Suppose A=∫dxx2+6x+25 and B=∫dxx2−6x−27.
If 12(A+B)=λ⋅tan−1(x+34)+μ⋅ln∣∣∣x−9x+3∣∣∣+C, then the value of (λ+μ) is ... .Solution in Punjabi
The correct Answer is:4
Step by step video & image solution for Suppose A=int (dx)/(x^(2)+6x+25) and B=int(dx)/(x^(2)-6x-27). If 12(A+B)=lambda*tan^(-1)((x+3)/(4))+mu* ln |(x-9)/(x+3)|+C, then the value of (lambda+mu) is ... . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Subjective Type Questions)
15 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHSCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise 5 ( Matching Type Questions )
2 Videos
- HYPERBOLABOOK - ARIHANT MATHSCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
The value of
∫e(xsinx+cosx).(x4cos3x−xsinx+cosxx2cos2x)dx, is equal to
View SolutionThe integral ∫sec2x(secx+tanx)92dx equals (for some arbitrary constant K).
View SolutionFind the mean marks of the following cummulative frequency table :
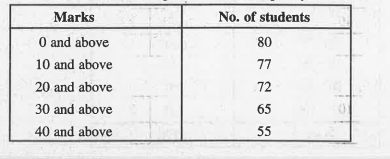

View Solutionwhich term of the following sequence : 312,3,332.....is 81?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View Solutionint(2)/((2-x)^(2))((2-x)/(2+x))^(1/3){dx=lambda((2+x)/(2-x))^(mu)+c where lambda and mu are rational number in its simplest form then (lambda+(1)/(mu)) is equal to
View Solutionint(2)/((2-x)^(2))((2-x)/(2+x))^(1/3)dx=lambda((2+x)/(2-x))^(mu)+c where lambda and mu are rational number in its simplest form then (lambda+(1)/(mu)) is equal to
View SolutionIf ∫1x3+x4dx=Ax2+Bx+log∣∣∣xx+1∣∣∣+C , then
View SolutionIf ∫ex(2−x2)(1−x)√1−x2dx=μex(1+x1−x)λ+C, then 2(λ+μ) is equal to ..... .
View SolutionSuppose A=∫dxx2+6x+25 and B=∫dxx2−6x−27.
If 12(A+B)=λ⋅tan−1(x+34)+μ⋅ln∣∣∣x−9x+3∣∣∣+C, then the value of (λ+μ) is ... .
View SolutionIf ∫6x+7(x+2)2dx=Alog|x+2|+Bx+2+c then, find the values of A and B.
View Solutionस्तम्भ (A)स्तम्भ(B)1.∫cotxdxa.12logx+c2.∫tanxdxb.12tanx+c3.∫dx1+cos2xc.log(sinx)+c4.∫(1+tan2x)dxd.log(secx)+c5.∫cosecxdxe.tanx+cf.log(tan.x2)+c
View Solution∫x−1(x−3)(x−2)dx=Aln(x−3)+Bln(x−2)+c, then find the value of A+B
View SolutionIf the integral I=∫dxx10+x=λln(x91+xμ)+C, (where, C is the constant of integration) then the value of 1λ+μ is equal to
View Solution(a) ∫x3(logx)2dx (b) ∫x3ex2dx
View SolutionIf ∫ex(2−x2)(1−x)√1−x2dx=μex(1+x1−x)λ+C, then 2(λ+μ) is equal to ..... .
View Solution
