Let O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as itsSolution in Punjabi
centroid
orthogonal
incentre
circumcentre
The correct Answer is:B
Step by step video & image solution for Let O be the origin and let PQR be an arbitrary triangle. The point S is such that bar(OP)*bar(OQ)+bar(OR)*bar(OS)=bar(OR)*bar(OP)+bar(OQ)*bar(OS)=bar(OQ)*bar(OR)+bar(OP)*bar(OS) Then the triangle PQR has S as its by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Subjective Type Questions)
18 Videos
- PROBABILITYBOOK - ARIHANT MATHSCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
55 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
For any two vectors →a and →b, prove that ∣∣→a.→b∣∣≤|→a|∣∣→b∣∣ Also write the name of this inequality.
View Solutionfind the derivative of sin x cos x
View SolutionProve that 2sin2(π6)−sec2(π3)=−72
View SolutionIf bar(PO)+bar(OQ)=bar(QO)+bar(OR), then prove that the points P,Q and R are collinear.
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that bar(OP)*bar(OQ)+bar(OR)*bar(OS)=bar(OR)*bar(OP)+bar(OQ)*bar(OS)=bar(OQ)*bar(OR)+bar(OP)*bar(OS) Then the triangle PQR has S as its
View SolutionLet PQRS be a parallelogram whose diagonals PR and QS intersect at O'. IF O is the origin then : ¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR+¯¯¯¯¯¯OS=
View Solutionमाना कि O मुलबिन्दु है एवं PQR एक स्वेच्छिक त्रिभुज है | बिन्दु S इस प्रकार है कि
−−→OP.−−→OQ+−−→OR.−−→OS=−−→OR.−−→OP+−−→OQ.−−→OS=−−→OQ.−−→OR+−−→OP.−−→OS
तब बिन्दु S त्रिभुज PQR का है
View SolutionO is the origin , P(2,3,4), Q(1,k,1) are points such that ¯¯¯¯¯¯OP⊥¯¯¯¯¯¯OQ then find k.
View SolutionIn the following map bar OP, bar OQ, bar OR And bar OS S are 4 rays /_POQ +/_ QOR + /_SOR + /_POS =360^(0) Prove that.
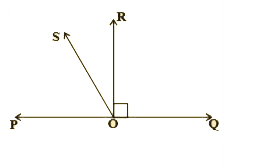
View SolutionIn the given figure ¯¯¯¯¯¯PQ is a line. Ray ¯¯¯¯¯¯OR is perpendicular to line ¯¯¯¯¯¯PQ.¯¯¯¯¯¯OS is another ray lying between rays ¯¯¯¯¯¯OPand ¯¯¯¯¯¯OR . Prove that ∠ROS=12∠QOS−∠POS
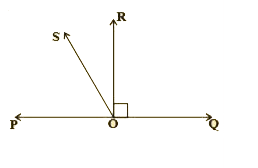
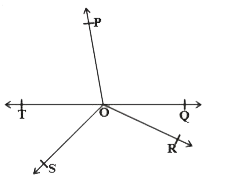
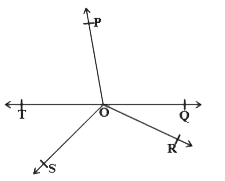
View SolutionIn the adjacent figure ¯¯¯¯¯¯OP,¯¯¯¯¯¯OQ,¯¯¯¯¯¯OR and¯¯¯¯¯¯OS are four rays. Prove that
∠POQ+∠QOR+∠SOR+∠POS=360∘ .
View SolutionIn the given figure ¯¯¯¯¯¯PQ is a line. Ray ¯¯¯¯¯¯OR is perpendicular to line ¯¯¯¯¯¯PQ.¯¯¯¯¯¯OS is another ray lying between rays ¯¯¯¯¯¯OPand ¯¯¯¯¯¯OR . Prove that ∠ROS=12∠QOS−∠POS
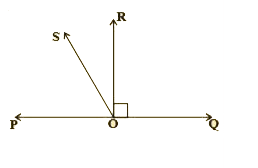
View SolutionIn the adjacent figure ¯¯¯¯¯¯OP,¯¯¯¯¯¯OQ,¯¯¯¯¯¯OR and¯¯¯¯¯¯OS are four rays. Prove that
∠POQ+∠QOR+∠SOR+∠POS=360∘ .
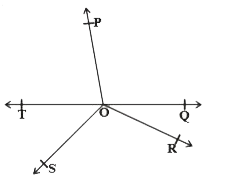
View SolutionIn the given figure ¯¯¯¯¯¯PQ is a line. Ray ¯¯¯¯¯¯OR is perpendicular to line ¯¯¯¯¯¯PQ.¯¯¯¯¯¯OS is another ray lying between rays ¯¯¯¯¯¯OPand ¯¯¯¯¯¯OR . Prove that ∠ROS=12∠QOS−∠POS
View SolutionIn the adjacent figure ¯¯¯¯¯¯OP,¯¯¯¯¯¯OQ,¯¯¯¯¯¯OR and¯¯¯¯¯¯OS are four rays. Prove that
∠POQ+∠QOR+∠SOR+∠POS=360∘ .
View SolutionIn the given figure ¯¯¯¯¯¯PQ is a line. Ray ¯¯¯¯¯¯OR is perpendicular to line ¯¯¯¯¯¯PQ.¯¯¯¯¯¯OS is another ray lying between rays ¯¯¯¯¯¯OPand ¯¯¯¯¯¯OR . Prove that ∠ROS=12∠QOS−∠POS

View Solution
