587 315 is written as 590 000 aftere it has been rounded off to
the nearest ten
the nearest hundred
the nearest thousand
the nearest ten thousand
To determine to what place the number 587315 has been rounded off to become 590000, we can follow these steps:
1. Identify the Original Number and the Rounded Number:
- The original number is 587315.
- The rounded number is 590000.
2. Determine the Difference Between the Original and Rounded Number:
- We can see that 590000 is greater than 587315. The difference is:
590000−587315=2685
3. Analyze the Rounded Number:
- The rounded number 590000 has three zeros at the end, which indicates that it has been rounded to the nearest ten thousand.
4. Check the Digit in the Ten Thousand Place:
- In the original number 587315, the digit in the ten thousand place is 8 (from 580000).
- The next digit (thousands place) is 7.
5. Apply Rounding Rules:
- According to rounding rules, if the digit in the thousands place (7) is 5 or greater, we round up the ten thousand place (8) by 1.
- Therefore, 8 becomes 9.
6. Conclusion:
- Since the digit in the thousands place was 7 (which is greater than 5), we rounded up the 8 in the ten thousand place to 9.
- Thus, 587315 rounded to the nearest ten thousand is 590000.
Final Answer: The number 587315 is rounded off to the nearest ten thousand.
- The original number is 587315.
- The rounded number is 590000.
- We can see that 590000 is greater than 587315. The difference is:
590000−587315=2685
- The rounded number 590000 has three zeros at the end, which indicates that it has been rounded to the nearest ten thousand.
- In the original number 587315, the digit in the ten thousand place is 8 (from 580000).
- The next digit (thousands place) is 7.
- According to rounding rules, if the digit in the thousands place (7) is 5 or greater, we round up the ten thousand place (8) by 1.
- Therefore, 8 becomes 9.
- Since the digit in the thousands place was 7 (which is greater than 5), we rounded up the 8 in the ten thousand place to 9.
- Thus, 587315 rounded to the nearest ten thousand is 590000.
Topper's Solved these Questions
- NUMBER SYSTEM - IBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM - IEXERCISE - HOTS WORKSHEET
20 Videos
- NUMBER SYSTEM - IBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM - IEXERCISE - IIT JEE WORKSHEET
32 Videos
- NUMBER SYSTEM - IBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM - IEXERCISE - CONCEPTIVE WORKSHEET
270 Videos
- MENSURATIONBOOK - BETOPPERSCHAPTER - MENSURATIONEXERCISE - IIT JEE WORKSHEET
16 Videos
- NUMBER SYSTEM-IIBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM-IIEXERCISE - IIT JEE WORKSHEET
51 Videos
Similar Questions
Study the following information to answer the given questions.
In a certain code, her idea has merit is written as fo la bu na, merit list has been displayed is written'as jo ke la si. na, her name displayed there is written as ya si bu zo and name in merit list is written as na ya go ke.
What does ke stand for?
1) been
2) has
3) merit
4) name
5) list
View SolutionWhat Journal entries would be passed for the following transactions on the dissolution of a firm of partners A and B :
(i) Old furniture which had been written off in the books was sold for ₹ 20,000 .
(ii) 'Z' an old customer whose account for ₹ 10 ,000 was written off as bad debt in the previous year paid 70%.
(iii) 'A' agreed to takeover firm's goodwill (Not recorded in the books of a firm ) at ₹ 50,000 .
(iv) There was an old computer which had been written off from the books . It was estimated to realise ₹ 5,000 .It is taken by B' a partner at the estimated price less 30 %.
(v) Investments costing ₹ 20 ,000 (being 1,000 shares ) , had been written off from the books . These investments (shares) are valued @ ₹ 15 each and divided among the partners in their profit-sharing ratio.
View Solution
Knowledge Check
A letter has been written by me.
AI have been writing a letter.BI has written a letter.CI had written a letter.DI have written a letter.The distance between two points is measured as 2.784843 m. This is to be rounded off to 4 significant figures. Hence the value of the distance should be written as
A2.784 mB2.785 mC2.7848 mD2.7849 m160 cycles were sold for Rs. 524,000 resulting in a loss of 10% What was the cost price of a cycle (in Rs.)?(rounded off to the nearest rupee)
A3275B3639C4321D4763
Pass the rectifying entries for the following transactions:
(i) An amount of Rs. 2,000 received from Mohan on 1st April, 2019 had been entered in the Cash Book as having been received on 31st March, 2019.
(ii) The balance in the account of Rahim Rs. 1,000 had been written off as bad but no other account has been debited.
(iii) An addition in the Return Inward Book had been cast Rs. 100 short.
(iv) A cheque for Rs. 200 drawn for the Petty Cash Account has been posted in the account of Asif.
(v) A discounted Bill of Exchange for Rs. 20,000 returned by the firm's bank had been credited to the Bank Account and debited to Bills Receivable Account. A cheque was received later from the customer for Rs. 20,000 and duly paid.
[Hint: (v) Dr. Customer's A/c and Cr. Bills Receivable A/c by Rs. 20,000.]
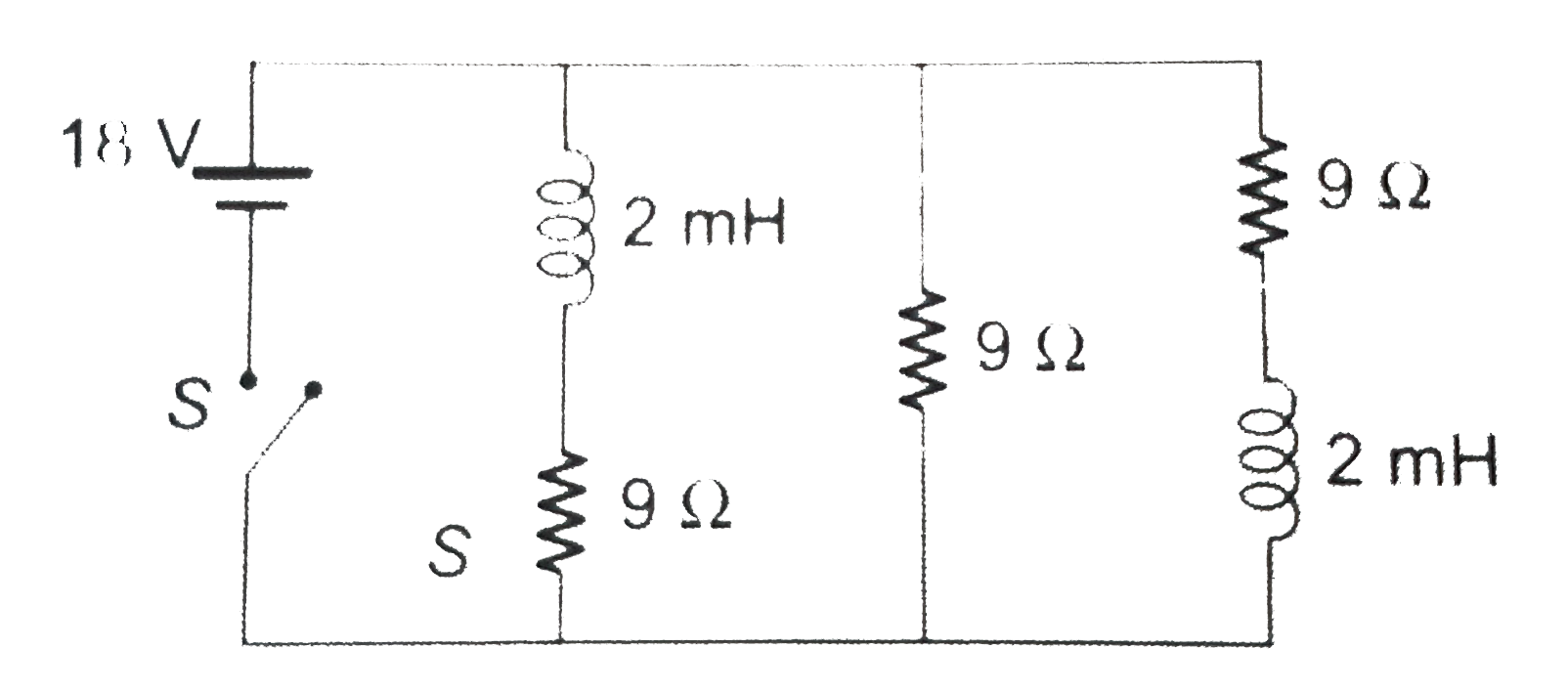
View SolutionFind current through the battery
(a) just after the switch is closed
(b) long after the switch has been closed
View Solution160 cycles were sold for Rs. 524,000 resulting in a loss of 10% What was the cost price of a cycle (in Rs.)?(rounded off to the nearest rupee)
View SolutionCompany 'A' has profit afterw tax, ₹1,50,000 and its number of equity shares is 10,000. Company 'B' has profits after tax, ₹1,20,000. and its numgber of shares is 12,000. which company has better EPS and how much ?
View SolutionSystema Naturae has been written by
View Solution
