A mountain peak in Himalayas has an elevation of 14,393 feet above sea level. A deep-sea trench in the Pacific Ocean has an elevation of 12, 456 feet below sea level. Find the difference in elevation between these two points.
To find the difference in elevation between the mountain peak in the Himalayas and the deep-sea trench in the Pacific Ocean, we can follow these steps:
Step 1: Identify the elevations
- The elevation of the mountain peak in the Himalayas is 14,393 feet above sea level.
- The elevation of the deep-sea trench in the Pacific Ocean is 12,456 feet below sea level.
Step 2: Convert the below sea level elevation to a positive value
Since the trench is below sea level, we can represent this elevation as a negative value:
- Below sea level = -12,456 feet
Step 3: Calculate the difference in elevation
To find the difference in elevation between the two points, we need to add the absolute values of the two elevations:
- Difference = Elevation of mountain peak - Elevation of trench
- Difference = 14,393 feet - (-12,456 feet)
- This is equivalent to:
14,393+12,456
Step 4: Perform the addition
Now, we can add the two values:
14,393+12,456=26,849 feet
Final Answer
The difference in elevation between the mountain peak and the deep-sea trench is 26,849 feet.
---
- The elevation of the mountain peak in the Himalayas is 14,393 feet above sea level.
- The elevation of the deep-sea trench in the Pacific Ocean is 12,456 feet below sea level.
Since the trench is below sea level, we can represent this elevation as a negative value:
- Below sea level = -12,456 feet
To find the difference in elevation between the two points, we need to add the absolute values of the two elevations:
- Difference = Elevation of mountain peak - Elevation of trench
- Difference = 14,393 feet - (-12,456 feet)
- This is equivalent to:
14,393+12,456
Now, we can add the two values:
14,393+12,456=26,849 feet
The difference in elevation between the mountain peak and the deep-sea trench is 26,849 feet.
Topper's Solved these Questions
- NUMBER SYSTEM - IBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM - IEXERCISE - IIT JEE WORKSHEET
32 Videos
- NUMBER SYSTEM - IBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM - IEXERCISE - SUMMATIVE WORKSHEET
54 Videos
- MENSURATIONBOOK - BETOPPERSCHAPTER - MENSURATIONEXERCISE - IIT JEE WORKSHEET
16 Videos
- NUMBER SYSTEM-IIBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM-IIEXERCISE - IIT JEE WORKSHEET
51 Videos
Similar Questions
Knowledge Check
The point A is on a mountain which is 5,700 metres above sea level and the point B is in a mine which is 39,600 meters below sea level. Find the vertical distance between A and B.
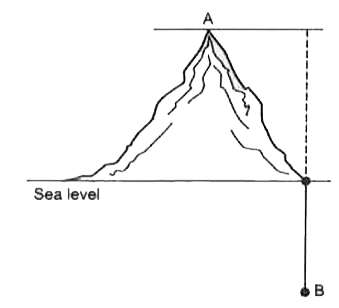 A42,300mB45,300mC46,300mD45,500m
A42,300mB45,300mC46,300mD45,500mAn aeroplane is vertically above the another plane flying at a height of 5000 feet from the ground. The angle of elevation of these two planes from a points on the ground are respectively π3andπ4. What is the vertical distance between these two planes ?
A2500(√3+1) feetB5000√3 feetC5000(√3−1) feetD5000(√3+1) feet
Height of a place A is 1800 m above sea level. Another place B is 700 m below sea level. What is the difference between the levels of these two places?
View SolutionA plane is flying at the height of 5000 m above the sea level. At aparticular point, it is exactly above a submarine floating 1200 m belowthe sea level. What is the vertical distance between them?
View SolutionThe highest point measured above sea level is the summit of Mt. Everest which is 8,848m above sea level and the lowest point is challenger Deep at the bottom of Mariana Trench which is 10911m below sea level. What is the vertical distance between these two points?
View SolutionThe marianas Trench, a region at the bottom of the Pacific Ocean is believed to be the deepest spot on the ocean floor. In 1960. a U.S Navy submersible vehicle werit to a spot in this Trench that is 10.700 m below sea level. Suppose the submarine had a tiny window of area 1cm2 so that sailors could enjoy the view. Find the force on this window due to the water pressure. Comment on the result.
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground lenvel and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown i fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass? Explain.

View SolutionThe table given below shows the elevations relative to sea level of four locations.
Taking sea level as zero, answer the following questions:

Arrange the locations from the least to the greatest elevation.
View Solution
