Given PQR is a straight line and
PQ : QR = 37.
Find QR : PQ
To solve the problem, we need to find the ratio QR : PQ given that PQ : QR = 37 : 1.
1. Understand the Given Ratio:
We are given that PQ : QR = 37 : 1. This means that for every 37 parts of PQ, there is 1 part of QR.
2. Write the Ratio in Fraction Form:
We can express the ratio PQ : QR as a fraction:
PQQR=371
3. Find the Reciprocal of the Ratio:
To find QR : PQ, we need to take the reciprocal of the given ratio. The reciprocal of a fraction is obtained by swapping the numerator and the denominator:
QR:PQ=QRPQ=137
4. Express the Ratio:
Thus, we can express QR : PQ as:
QR:PQ=1:37
Final Answer:
QR : PQ = 1 : 37
---
We are given that PQ : QR = 37 : 1. This means that for every 37 parts of PQ, there is 1 part of QR.
We can express the ratio PQ : QR as a fraction:
PQQR=371
To find QR : PQ, we need to take the reciprocal of the given ratio. The reciprocal of a fraction is obtained by swapping the numerator and the denominator:
QR:PQ=QRPQ=137
Thus, we can express QR : PQ as:
QR:PQ=1:37
QR : PQ = 1 : 37
Topper's Solved these Questions
- RATIO AND PROPORTIONBOOK - BETOPPERSCHAPTER - RATIO AND PROPORTIONEXERCISE - SUMMATIVE WORKSHEET
31 Videos
- RATIO AND PROPORTIONBOOK - BETOPPERSCHAPTER - RATIO AND PROPORTIONEXERCISE - HOTS WORKSHEET
19 Videos
- RATIO AND PROPORTIONBOOK - BETOPPERSCHAPTER - RATIO AND PROPORTIONEXERCISE - IIT JEE WORKSHEET
1 Videos
- NUMBER SYSTEM-IIBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM-IIEXERCISE - IIT JEE WORKSHEET
51 Videos
Similar Questions
Knowledge Check
PQR is an isosceles triangle with sides PQ=PR=45cmand QR=72cm. PN is a median to base QR. What will be the length (in cm.) of PN?
A36B24C27D32PQR is an isosceles triangle with sides PQ=PR=45cmand QR=72cm. PN is a median to base QR. What will be the length (in cm.) of PN?
A36B24C27D32In ∠PQR,PQ=6cm,PR=9cm and M is a point on QR such that it divides QR in the ratio 1:2PM⊥QR. Find QR.
A√18 cmB3√12 cmC3√15 cmD√20 cm
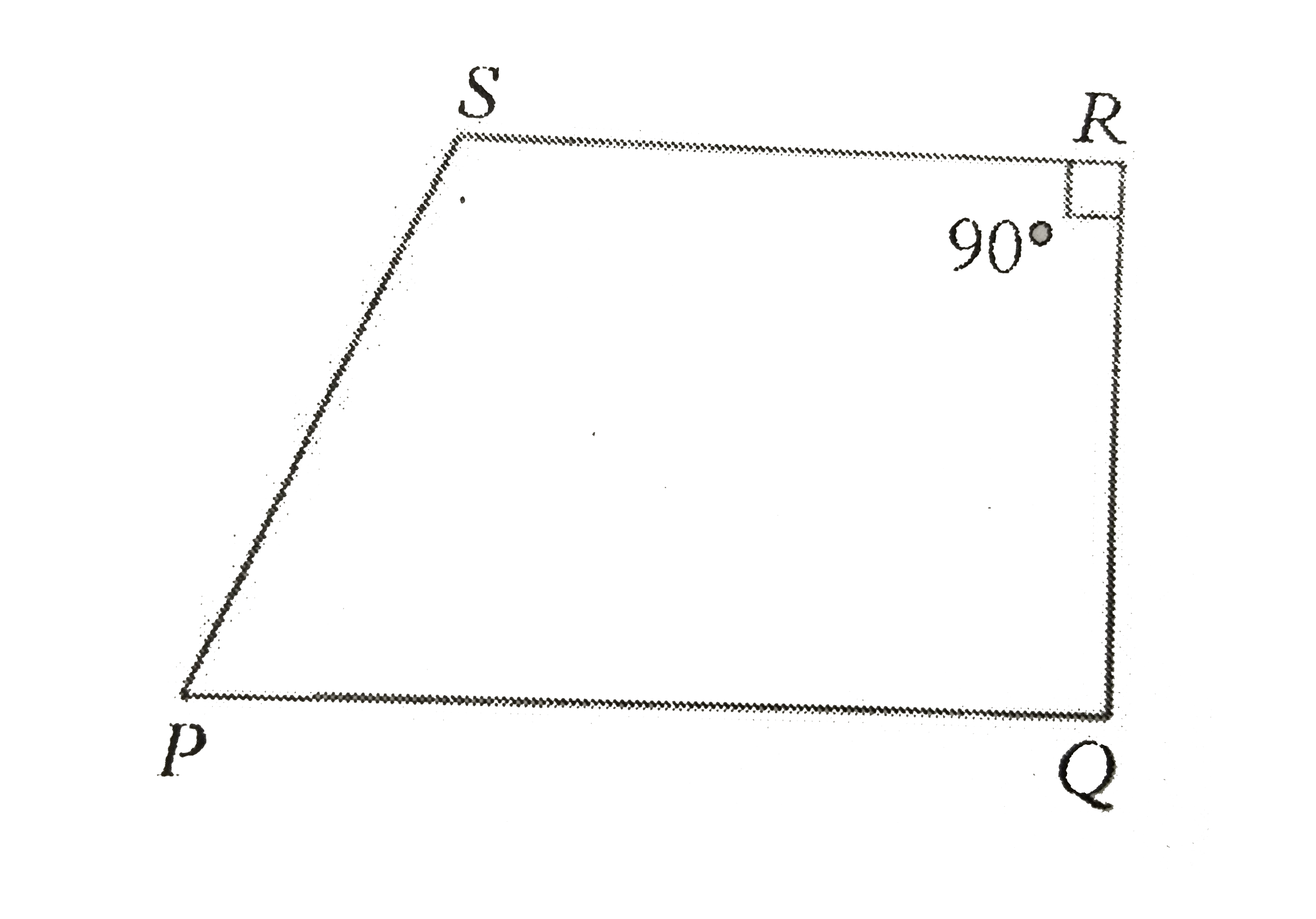
In the figure above, PQRS is a trapezium , PQ//SR, QR=RS, and ∠QRS=90∘. If QR=24 cm and PS=25 cm , then find the length of PQ.
View SolutionPQR is a triangle right angled at P. If PQ=10cmandPR=24cm, find QR
View SolutionIn the given figures □PQRS is rectangle . If PQ=14, QR =21 cm , Find the area of the parts x,y and z
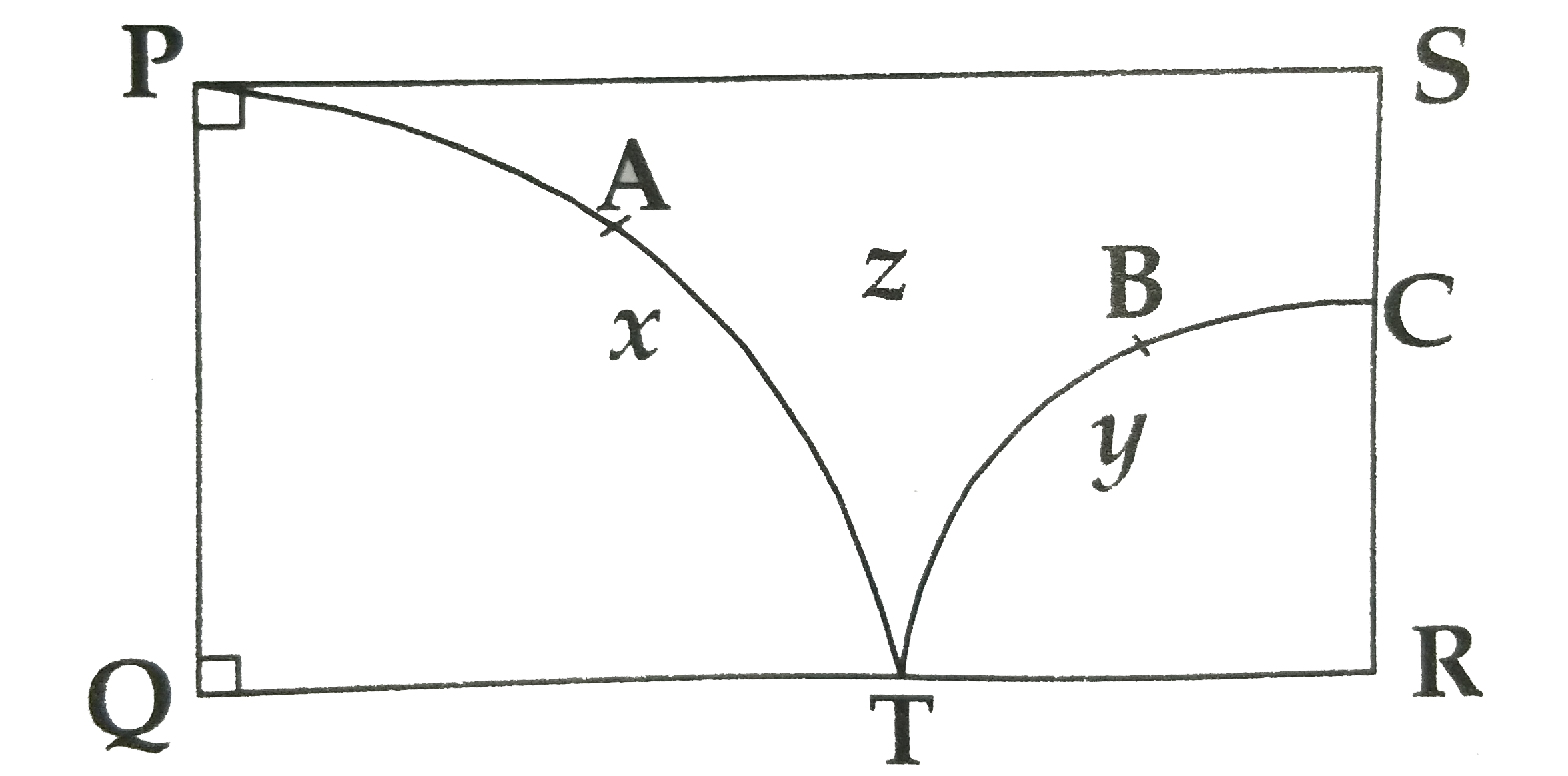
Given □PQRS is reactangle
PQ=14cm, QR=21cm
To find: x, y and z
View SolutionIn ΔABC, the line parallel to BC Intersects AB and AC at P and Q respectively. If AB:AP=5:3then AQ:QCis :
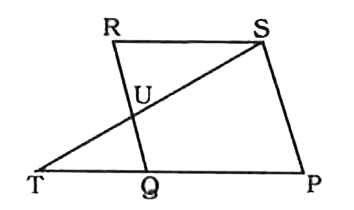
View SolutionIn the given figure, PQRSis a parallelogram and U is the mid point of QR. If PQ=4cm, then what is the value of PT (in cm.)?
View Solution

