For a rectangle with integral lengths of sides and 196 m2 area, the minimum perimeter is obtained by taking the length of the rectangle as
4m
7m
14m
28m
To solve the problem of finding the length of a rectangle with integral side lengths and an area of 196 m² that minimizes the perimeter, we can follow these steps:
1. Understand the Problem: We need to find the dimensions of a rectangle (length l and breadth b) such that the area A=l×b=196m2 and the perimeter P=2(l+b) is minimized.
Hint: Recall the formulas for area and perimeter of a rectangle.
2. Set Up the Equation: From the area equation, we can express one variable in terms of the other. Let's express b in terms of l:
b=196l
Hint: Rearranging the area formula helps us relate the two dimensions.
3. Express the Perimeter: Substitute b in the perimeter formula:
P=2(l+b)=2(l+196l)
Hint: This step combines both dimensions into one equation for perimeter.
4. Minimize the Perimeter: To minimize the perimeter, we need to find the value of l that minimizes P. To do this, we can differentiate P with respect to l and set the derivative to zero. However, since we are looking for integral values, we can also analyze the factors of 196.
Hint: Consider the factors of 196 to find pairs of (l,b).
5. Find Factors of 196: The factors of 196 are:
- 1×196
- 2×98
- 4×49
- 7×28
- 14×14
Hint: List all pairs of factors to explore possible dimensions.
6. Calculate Perimeters: Now calculate the perimeter for each pair of factors:
- For (1,196): P=2(1+196)=394
- For (2,98): P=2(2+98)=200
- For (4,49): P=2(4+49)=106
- For (7,28): P=2(7+28)=70
- For (14,14): P=2(14+14)=56
Hint: Calculate the perimeter for each factor pair to find the minimum.
7. Identify the Minimum Perimeter: From the calculations, the minimum perimeter is 56 when both length and breadth are 14.
Hint: Compare the calculated perimeters to find the smallest value.
8. Conclusion: The length of the rectangle that gives the minimum perimeter is 14m.
Final Answer: The minimum length of the rectangle is 14m.
b=196l
P=2(l+b)=2(l+196l)
- 1×196
- 2×98
- 4×49
- 7×28
- 14×14
- For (1,196): P=2(1+196)=394
- For (2,98): P=2(2+98)=200
- For (4,49): P=2(4+49)=106
- For (7,28): P=2(7+28)=70
- For (14,14): P=2(14+14)=56
Topper's Solved these Questions
- MENSURATIONBOOK - BETOPPERSCHAPTER - MENSURATIONEXERCISE - CONCEPTIVE WORKSHEET
25 Videos
- MENSURATIONBOOK - BETOPPERSCHAPTER - MENSURATIONEXERCISE - SUMMATIVE WORKSHEET
7 Videos
- ALGEBRABOOK - BETOPPERSCHAPTER - ALGEBRAEXERCISE - IIT JEE WORKSHEET
23 Videos
- NUMBER SYSTEM - IBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM - IEXERCISE - IIT JEE WORKSHEET
32 Videos
Similar Questions
Knowledge Check
The area of a square is 900cm2. The length of a rectangle is equal to the side of the given square and breadth of the rectangle is equal to half the length of the rectangle. The area of rectangle is
A450cm2B500cm2C445cm2D490cm2The areas of a square and a rectangle are equal. The length of the rectangle is greater than the length of any side of the square by 5 cm and the breadth is less by 3 cm. Find the perimeter of the rectangle.
A17 cmB26 cmC30 cmD34 cmThe length and breadth of a rectangle is in the ratio of 3:1 .If its perimeter is 96 m ,then what is the length of the rectangle ?
A36 mB24 mC12 mD48 m
The length of a rectangle is two times its breadth. Its perimeter is 60 cm.
If the breadth of rectangle is x cm, the length of the rectangle is ________.
View SolutionThe maximum area of a rectangle with integral lengths and having a perimeter 36 m is
View SolutionThe area of a square and a rectangle are equal. If the side of the square is40 cm and the breadth of the rectangle is 25 cm, find the length of therectangle. Also, find the perimeter of the rectangle.
View SolutionThe area of a square and a rectangle are equal.If the side of the square is 40 cm and the breadth of the rectangle is 25 cm,find the length of the rectangle. Also,find the perimeter of the rectangle.
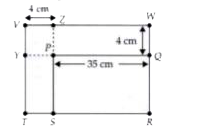
View SolutionPQRS is a rectangle. When the length and breadth of the rectangle increases, the rectangle is enlarged to VWRT and the area of the rectangle is enlarged by 226cm2. If the length of rectangle PQRS is twice its breadth. Find
(i) Perimeter of rectangle PQRS.
(ii) Area of rectangle VWRT.
View Solution
