With the help of Venn diagram prove that A∪(B∩C)=(A∪B)∩(A∪C)
Video Solution
|
Answer
Step by step video & image solution for With the help of Venn diagram prove that Auu(BcapC)=(AuuB)cap(AuuC) by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Which of the following Venn diagram represent (A−B)?
A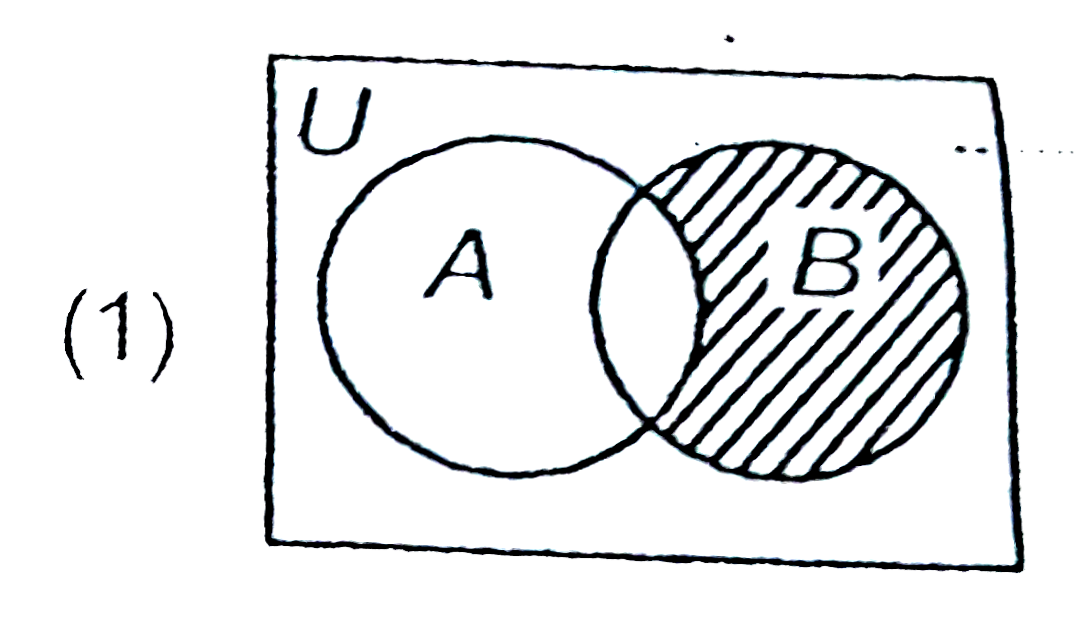 B
B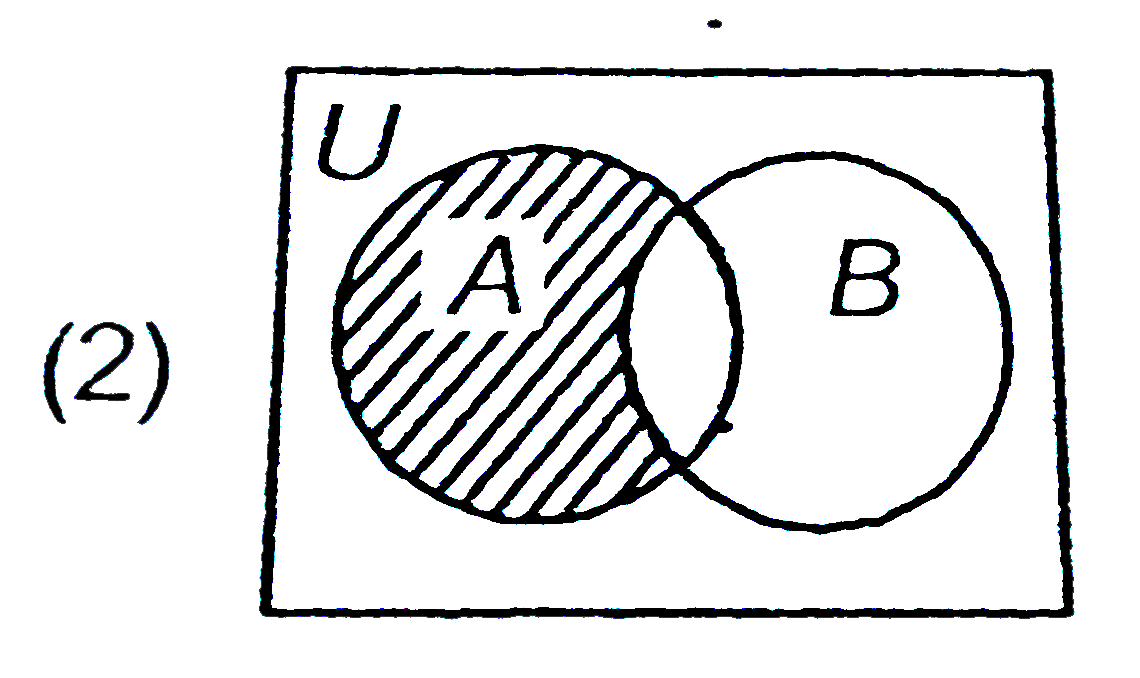 C
C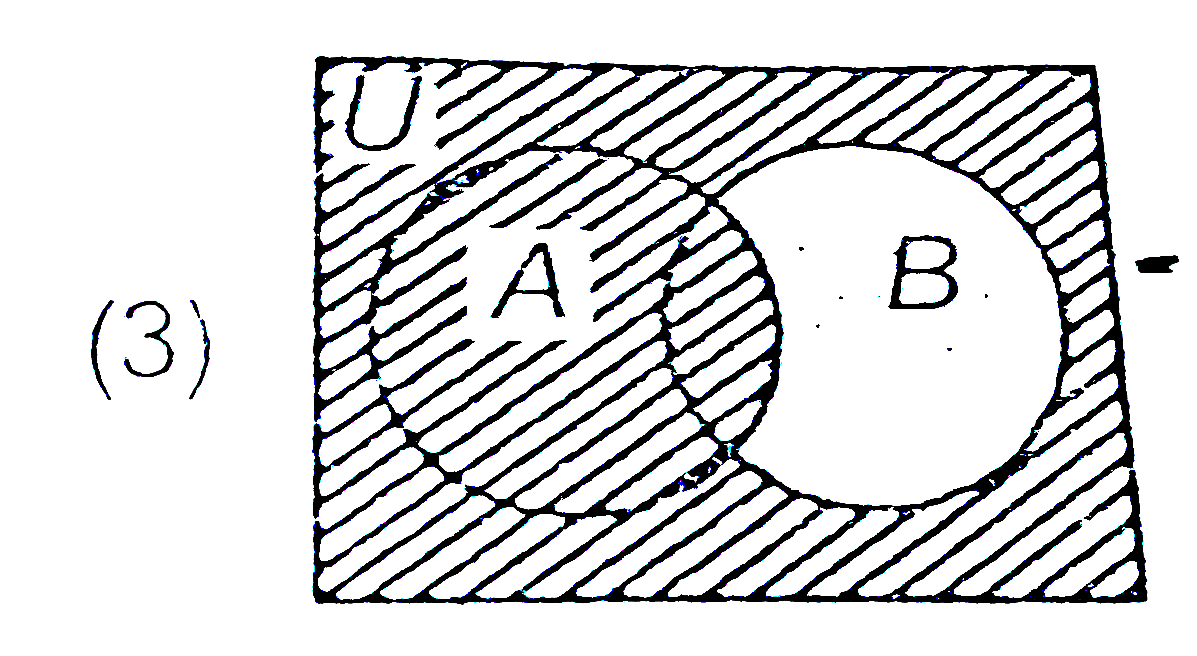 D
D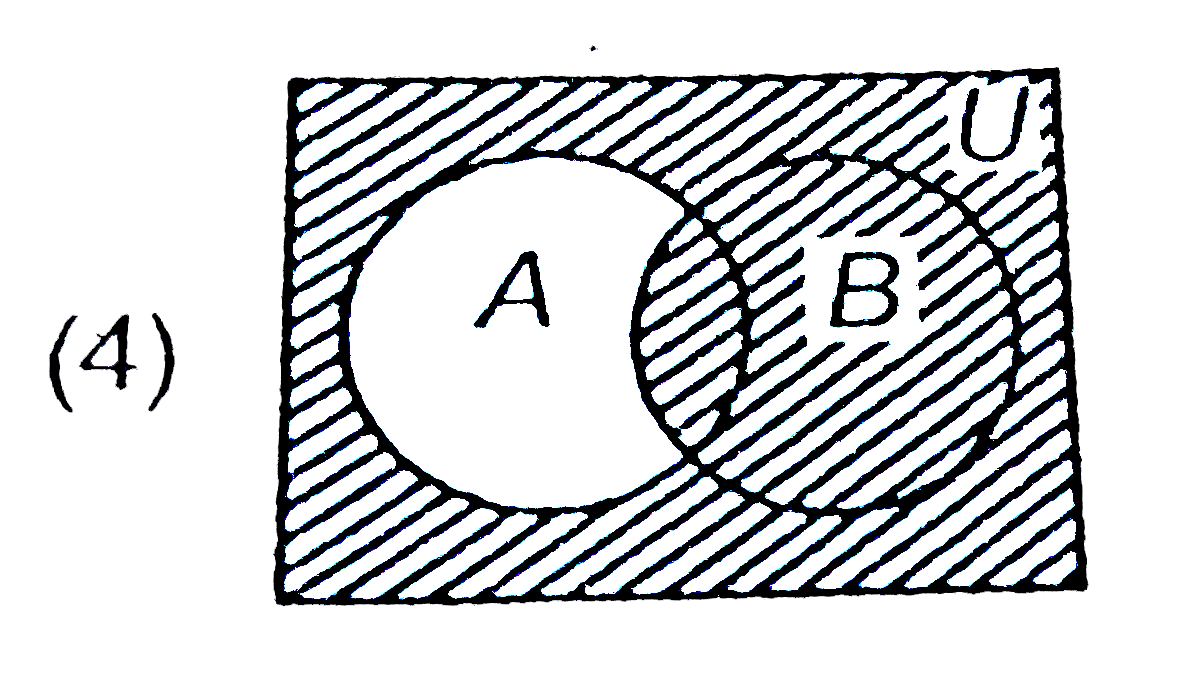
Prove A∪(B∩C)=(A∪B)∩(A∪C)
View SolutionProve that (A∪B)−(A∩B)=(A−B)∪(B−A).
View SolutionProve that A−B=A∩B'.
View SolutionVerify the following identities :
(i) A∪(B∩C)=(A∪B)∩(A∪C)
(ii) A∩(B∪C)=(A∩B)∪(A∩C),
where A,B and C are three sets defined by :
A={1,2,4,5},B={2,3,5,6}
C= {4,5,6,7}.
View SolutionStudy the given Venn diagram carefully.
View SolutionIf A={1,2,3},B={4,5,6} and
C=(7,8,9} , verify that :
A∪(B∩C)=(A∪B)∩(A∪C).
View SolutionFor any 3 sets A, B and C, prove that :
(i) A−(B∪C)=(A−B)∩(A−C)
(ii) A−(B∩C)=(A−B)∪(A−C)
(iii) A∩(B−C)=(A∩B)−(A∩C)
(iv) (A∪B)−C=(A−C)∪(B−C)
(v) A∩(BΔC)=(A∩B)Δ(A∩C).
View Solution
