The remainder when 625 is divided by 13 is
1
7
3
9
To find the remainder when 625 is divided by 13, we can follow these steps:
Step 1: Perform the Division
First, we need to divide 625 by 13. We can do this by estimating how many times 13 fits into 625.
Step 2: Estimate the Quotient
We can start by estimating how many times 13 fits into 625.
- 13 × 4 = 52
- 13 × 5 = 65
- 13 × 6 = 78
- 13 × 7 = 91
- 13 × 8 = 104
- 13 × 9 = 117
- 13 × 10 = 130
- 13 × 20 = 260
- 13 × 30 = 390
- 13 × 40 = 520
- 13 × 50 = 650 (too high)
From this, we see that 13 fits into 625 approximately 48 times, since 13 × 48 = 624.
Step 3: Calculate the Product
Now, we calculate the product of 13 and 48:
- 13 × 48 = 624
Step 4: Find the Remainder
Next, we subtract this product from 625 to find the remainder:
- Remainder = 625 - 624 = 1
Conclusion
Thus, the remainder when 625 is divided by 13 is 1.
First, we need to divide 625 by 13. We can do this by estimating how many times 13 fits into 625.
We can start by estimating how many times 13 fits into 625.
- 13 × 4 = 52
- 13 × 5 = 65
- 13 × 6 = 78
- 13 × 7 = 91
- 13 × 8 = 104
- 13 × 9 = 117
- 13 × 10 = 130
- 13 × 20 = 260
- 13 × 30 = 390
- 13 × 40 = 520
- 13 × 50 = 650 (too high)
Now, we calculate the product of 13 and 48:
- 13 × 48 = 624
Next, we subtract this product from 625 to find the remainder:
- Remainder = 625 - 624 = 1
Thus, the remainder when 625 is divided by 13 is 1.
Similar Questions
Knowledge Check
Find the remainder when 599 is divided by 13.
A6B8C9D10The remainder when 54n is divided by 13, is
A1B8C9D10When n is divided by 4, the remainder is 3. The remainder when 2n is divided by 4 is :
Aa) 1Bb) 2Cc) 3Dd) 6
Find the remainder when 2515 is divided by 13.
View SolutionUsing Binomial theorem, find the remainder when 5103 is divided by 13.
View SolutionThe remainder when n is divided by 3 is 1 and the remainder when (n+1) is divided by 2 is 1. The remainder when (n-1) is divided by 6 is :
View SolutionThe remainder when n is divided by 3 is 1 and the remainder when (n+1) is divided by 2 is 1. The remainder when (n-1) is divided by 6 is :
View SolutionThe remainder when
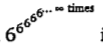 is divided by 10 is :
is divided by 10 is :
View Solution
