(723+1992)2−(723−1992)2÷723×1992=?
4
33
6
1
The correct Answer is:A
To solve the expression (723+1992)2−(723−1992)2÷723×1992, we will follow these steps:
1. Identify Variables: Let a=723 and b=1992. This simplifies our expression.
2. Rewrite the Expression: The expression can be rewritten as:
(a+b)2−(a−b)2÷(a×b)
3. Apply the Difference of Squares Formula: We can use the identity x2−y2=(x−y)(x+y) where x=(a+b) and y=(a−b):
(a+b)2−(a−b)2=((a+b)−(a−b))((a+b)+(a−b))
Simplifying each part:
- (a+b)−(a−b)=2b
- (a+b)+(a−b)=2a
Therefore, we have:
(a+b)2−(a−b)2=2b⋅2a=4ab
4. Substitute Back into the Expression: Now substitute 4ab back into the expression:
4ab÷(ab)
5. Simplify the Expression: The ab in the numerator and denominator cancels out:
4ab÷ab=4
Thus, the final answer is:
4
(a+b)2−(a−b)2÷(a×b)
(a+b)2−(a−b)2=((a+b)−(a−b))((a+b)+(a−b))
Simplifying each part:
- (a+b)−(a−b)=2b
- (a+b)+(a−b)=2a
(a+b)2−(a−b)2=2b⋅2a=4ab
4ab÷(ab)
4ab÷ab=4
4
Topper's Solved these Questions
Similar Questions
Knowledge Check
(723+1992)2−(723−1992)2÷723×1992=?
A4B33C6D1(8)2%of=723+45
A1200B1400C1100D1020Select the number which does not belong to the given series. 1956, 1968. 1976. 1982, 1988, 1992.
Aa. 1956Bb. 1976Cc. 1982Dd. 1992
Evaluate (72.3)13iflog0.723=1.8591.
View SolutionEvaluate: 3√72.3;iflog 0.723 = ¯1.8591
View Solutiondet∣∣ ∣∣199019911992199119921993199219931994∣∣ ∣∣=
View Solution[ The difference between the local value and face value of 6 in the numeral 586723 is: [ a) 723, b) 6717, c) 5994, d) None of these ]]
View SolutionFollowing table gives the population of a from 1998 to 1992
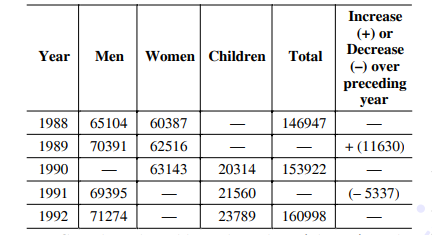
Number of women in 1991 is -----
View Solution
