Let a = BC, b = CA, c = AB be side lengths of a triangle ABC. And m be the length of the median through A. If a = 8, b-c = 2, m = 6, then the nearest integer to b is
7
8
9
10
The correct Answer is:B
Step by step video, text & image solution for Let a = BC, b = CA, c = AB be side lengths of a triangle ABC. And m be the length of the median through A. If a = 8, b-c = 2, m = 6, then the nearest integer to b is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-I (MATHEMATICS)
20 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( MATHEMATICS)
10 Videos
- SOLVED PAPER 2018BOOK - KVPY PREVIOUS YEARCHAPTER - SOLVED PAPER 2018EXERCISE - EXAMPLE
27 Videos
Similar Questions
Knowledge Check
Let a = BC, b = CA, c = AB be side lengths of a triangle ABC. And m be the length of the median through A. If a = 8, b-c = 2, m = 6, then the nearest integer to b is
A7B8C9D10Let a, b, c be the side-lengths of a triangle, and l, m,n be the lengths of its medians. Put K=(l+m+na+b+c) Then, as a, b, c vary, K can assume every value in the interval
A(14,45)B(12,45)C(34,1)D(45,54)The sides of a triangle ABC are 6, 7, 8, the smallest angle being C then
The length of the median from C isA√951B√952C√953Dnone
In a triangle ABC the length of the sides, AB is 3 m and BC is 5 m what is the length of AC, if the angle formed at B is 60∘
View SolutionLet →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
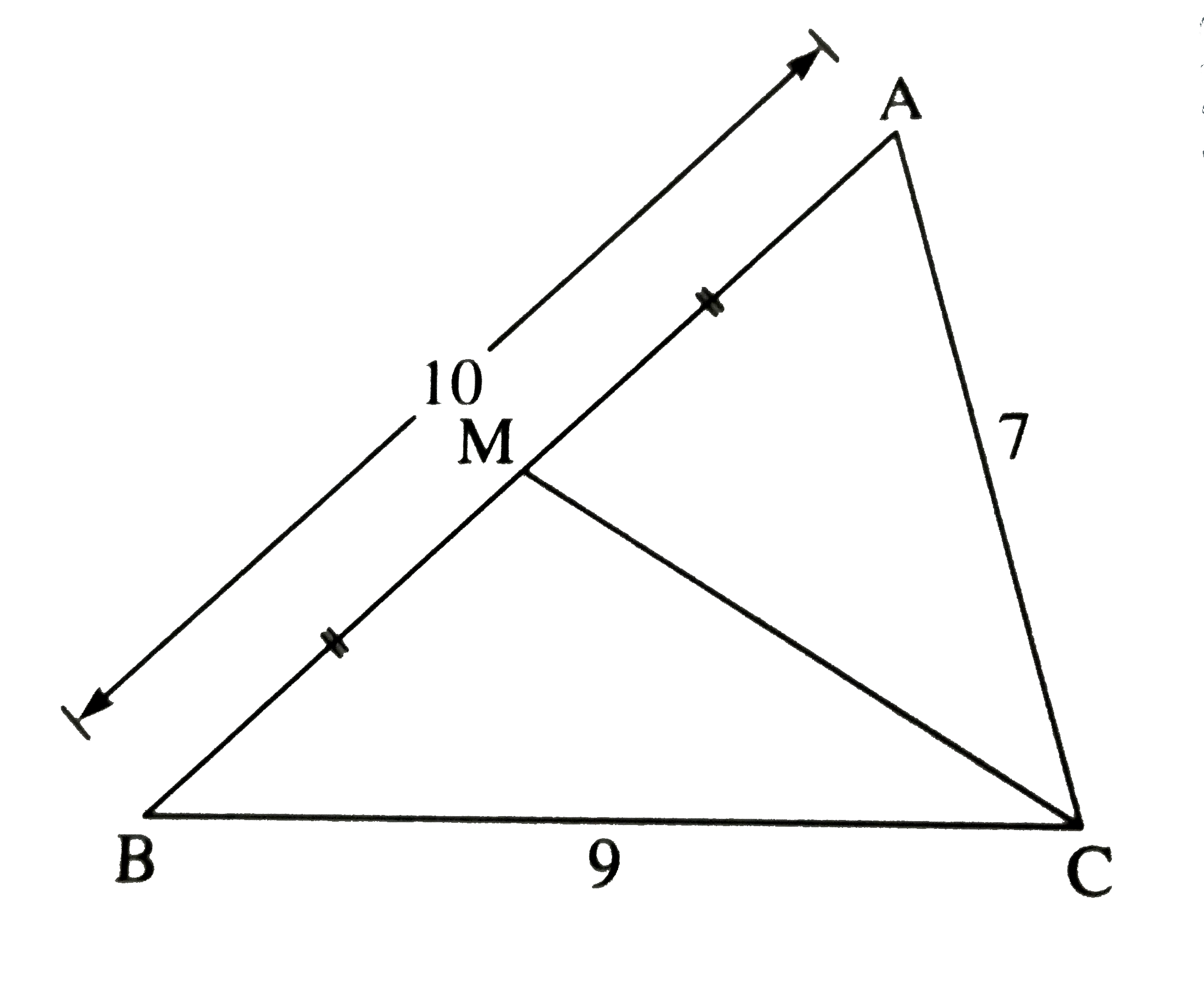
View SolutionIn △ABC , AB=10
AC=7,BC=9
then find the length find the length of the median drawn from point C to side AB .
View SolutionVertices of a ΔABC are A(2, 2), B (-4, -4) and C (5, -8) , then the length of the median through C is
View SolutionVertices of a ΔABC are A(2, 2), B (-4, -4) and C (5, -8) , then the length of the median through C is
View Solution