In a triangle ABC with ∠A<∠B<∠C, points D, E, F are on the interior of segments BC, CA, AB, respectively. Which of the following triangles CANNOT be similar to ABC?
Triangle ABD
Triangle BCE
Triangle CAF
Triangle DEF
The correct Answer is:A
To determine which triangle cannot be similar to triangle ABC given the conditions, we can follow these steps:
Step 1: Understand the properties of similar triangles
Two triangles are similar if their corresponding angles are equal and the ratios of their corresponding sides are proportional.
Hint: Remember that for triangles to be similar, both angle and side ratios must match.
Step 2: Identify the angles of triangle ABC
In triangle ABC, we know that angle A < angle B < angle C. This means:
- Angle A is the smallest,
- Angle B is the middle,
- Angle C is the largest.
Hint: The order of angles is crucial for determining similarity.
Step 3: Analyze triangle ABD
Let’s consider triangle ABD, where D is a point on segment BC. The angles in triangle ABD will be:
- Angle A (common),
- Angle ABD (which is not equal to angle B),
- Angle ADB (which is not equal to angle C).
Since angle ABD and angle ADB cannot match the angles of triangle ABC (because angle A is the smallest), triangle ABD cannot have the same angle configuration as triangle ABC.
Hint: Check if the angles in triangle ABD can correspond to those in triangle ABC.
Step 4: Compare the sides of triangle ABD with triangle ABC
For triangle ABD to be similar to triangle ABC, the ratios of the sides must also be proportional. However, since the angles do not match, the side ratios will also not satisfy the similarity condition.
Hint: If angles do not match, the side ratios cannot be proportional either.
Step 5: Conclusion
Since triangle ABD does not have the same angle configuration as triangle ABC, it cannot be similar to triangle ABC.
Final Answer: Triangle ABD cannot be similar to triangle ABC.
Two triangles are similar if their corresponding angles are equal and the ratios of their corresponding sides are proportional.
In triangle ABC, we know that angle A < angle B < angle C. This means:
- Angle A is the smallest,
- Angle B is the middle,
- Angle C is the largest.
Let’s consider triangle ABD, where D is a point on segment BC. The angles in triangle ABD will be:
- Angle A (common),
- Angle ABD (which is not equal to angle B),
- Angle ADB (which is not equal to angle C).
For triangle ABD to be similar to triangle ABC, the ratios of the sides must also be proportional. However, since the angles do not match, the side ratios will also not satisfy the similarity condition.
Since triangle ABD does not have the same angle configuration as triangle ABC, it cannot be similar to triangle ABC.
Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II (MATHEMATICS)
5 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-I ( MATHEMATICS)
20 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
25 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-II(MATHEMATICS)
10 Videos
Similar Questions
Knowledge Check
ABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
A4:1B5:1C3:1Dcan't be determindABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
A4:1B5:1C3:1Dcan't be determinedIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
A→BE+→CFB→BE−→CFC→CF−→BED−→BE−→CF
In a triangle ABC, AB=BC and ∠A=60∘. Find ∠B.
View SolutionIn figure, ∠B<∠A and ∠C<∠D. Show that AD<BC.
View SolutionIn the figure ∠B<∠Aand∠C<∠D. Show that AD<BC.
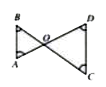
View SolutionIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
View SolutionFrom a point O in the interior of a DeltaABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
View Solution
