The number of rounds of a wire around a pencil are 24 and the length of the coil is 4.8cm then what is the diameter of wire ?
24cm
2.4 cm
20cm
0.2 cm
To find the diameter of the wire wrapped around the pencil, we can follow these steps:
Step 1: Understand the Problem
We are given:
- The number of turns (coils) of the wire around the pencil = 24
- The total length of the wire (length of the coil) = 4.8 cm
Step 2: Calculate the Length of One Turn
The length of one complete turn of the wire can be calculated by dividing the total length of the wire by the number of turns.
Length of one turn=Total length of wireNumber of turns=4.8cm24
Step 3: Perform the Calculation
Now, let's perform the calculation:
Length of one turn=4.824=0.2cm
Step 4: Relate the Length of One Turn to the Diameter of the Wire
The length of one turn of the wire is equal to the circumference of the wire. The circumference C of a circle is given by the formula:
C=π×d
Where d is the diameter of the wire. Therefore, we can set up the equation:
0.2cm=π×d
Step 5: Solve for the Diameter
To find the diameter d, we can rearrange the equation:
d=0.2π
Step 6: Calculate the Diameter
Using the value of π≈3.14:
d≈0.23.14≈0.0637cm
Final Answer
The diameter of the wire is approximately 0.0637cm.
---
We are given:
- The number of turns (coils) of the wire around the pencil = 24
- The total length of the wire (length of the coil) = 4.8 cm
The length of one complete turn of the wire can be calculated by dividing the total length of the wire by the number of turns.
Now, let's perform the calculation:
The length of one turn of the wire is equal to the circumference of the wire. The circumference C of a circle is given by the formula:
To find the diameter d, we can rearrange the equation:
Using the value of π≈3.14:
The diameter of the wire is approximately 0.0637cm.
Topper's Solved these Questions
- MEASUREMENTBOOK - BEIITIANSCHAPTER - MEASUREMENTEXERCISE - CONCEPTIVE WORKSHEET
71 Videos
- MEASUREMENTBOOK - BEIITIANSCHAPTER - MEASUREMENTEXERCISE - SUMMATIVE WORKSHEET
10 Videos
- HEATBOOK - BEIITIANSCHAPTER - HEATEXERCISE - IIT JEE Worksheet (V. Matrix Matching)
4 Videos
- MOTIONBOOK - BEIITIANSCHAPTER - MOTIONEXERCISE - IIT JEE WORKSHEET (MATIRX MATCHING)
1 Videos
Similar Questions
Knowledge Check
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108m, the diameter of the wire is
Aa) 1 cmBb) 0.9 cmCc) 0.3 cmDd) 0.6cmA wire is wound over a pencil and placed over a scale as shown in the figure. The diameter of the given wire is ________.
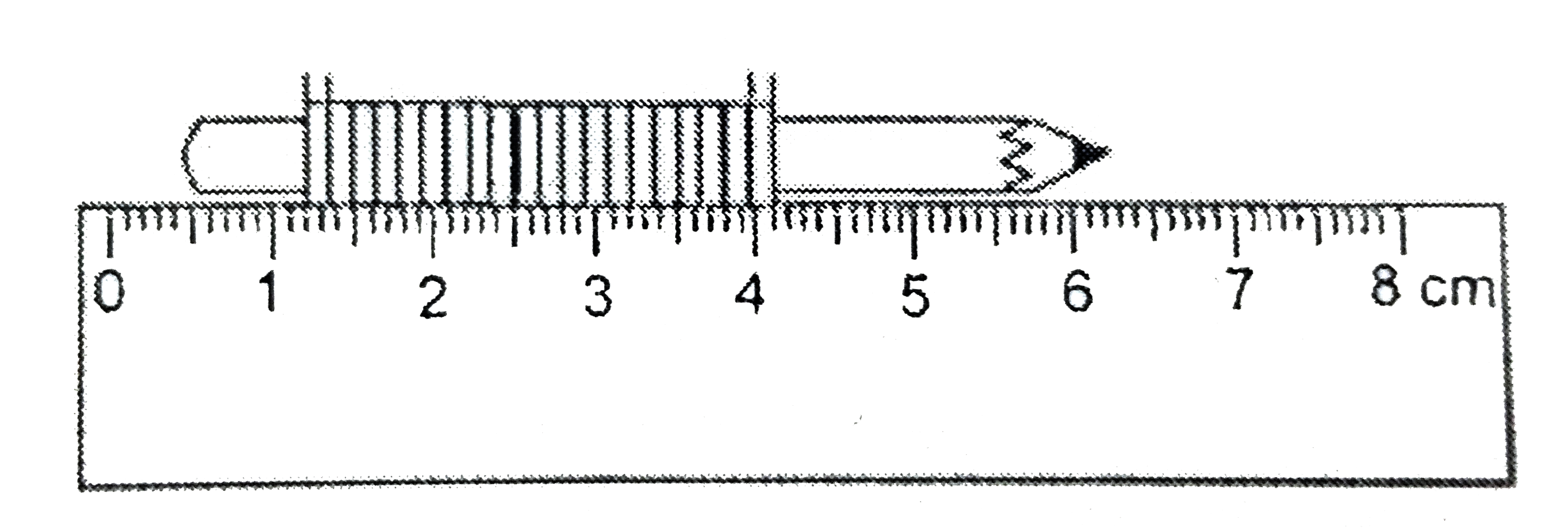 A1.45cmB2.9mmC2.9mD1.45mm
A1.45cmB2.9mmC2.9mD1.45mmA wire is wound over a pencil and placed over a scale as shown in the figure. The diameter of the given wire is ________.
 A1.45cmB2.9cmC2.9mD1.45mm
A1.45cmB2.9cmC2.9mD1.45mm
A sphere of radius 3 cm is drawn into a wire of thickness of 0.5 cm . What is the length of the wire ?
View SolutionTwo wires A and B equal mass and of the same metal are taken. The diameter of the wire A is half the diameter of wire B. If the resistance of wire A is 24Ω, calculatate the resistance of wire B.
View SolutionThe diameter of a copper sphere is 12 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 48 cm, find its diameter
View SolutionA solid sphere of diameter 60 mm is melted to stretch into a wire of length 144 cm. What is the diameter of the wire?
View SolutionWhen a weight of 5kg is suspended from a copper wire of length 30m and diameter 0.5mm, the length of the wire increases by 2.4cm. If the diameter is doubled, the extension produced is
View Solution
