In a circket match there are three types of tickets say A,B and C each costing Rs. 1,000 ,Rs. 500 and Rs. 200 respectively .The ratio of three ticket sold of category A,B and C is 3:2:5 . If the total collection from selling the tickets is Rs. 2.5 crore .find the total number of tickets sold ?
5000
4800
50000
52000
To solve the problem, we will follow these steps:
Step 1: Understand the ticket prices and the ratio
The prices of the tickets are:
- Ticket A: Rs. 1,000
- Ticket B: Rs. 500
- Ticket C: Rs. 200
The ratio of tickets sold is A:B:C = 3:2:5.
Step 2: Define the variables based on the ratio
Let the number of tickets sold for A, B, and C be:
- A = 3k
- B = 2k
- C = 5k
where k is a common multiplier.
Step 3: Calculate the total revenue from ticket sales
The total revenue from selling the tickets can be calculated as follows:
- Revenue from A = Number of A tickets × Price of A = 3k × 1000 = 3000k
- Revenue from B = Number of B tickets × Price of B = 2k × 500 = 1000k
- Revenue from C = Number of C tickets × Price of C = 5k × 200 = 1000k
Now, we can combine these to find the total revenue:
Total Revenue = Revenue from A + Revenue from B + Revenue from C
Total Revenue = 3000k + 1000k + 1000k = 5000k
Step 4: Set up the equation for total collection
We know that the total collection from selling the tickets is Rs. 2.5 crore, which is Rs. 2,50,00,000. Therefore, we can set up the equation:
5000k = 2,50,00,000
Step 5: Solve for k
To find k, we divide both sides of the equation by 5000:
k = 2,50,00,000 / 5000
k = 50,000
Step 6: Calculate the total number of tickets sold
Now that we have k, we can find the total number of tickets sold:
Total tickets = A + B + C = 3k + 2k + 5k = 10k
Total tickets = 10 × 50,000 = 5,00,000
Final Answer
The total number of tickets sold is 5,00,000.
---
The prices of the tickets are:
- Ticket A: Rs. 1,000
- Ticket B: Rs. 500
- Ticket C: Rs. 200
Let the number of tickets sold for A, B, and C be:
- A = 3k
- B = 2k
- C = 5k
The total revenue from selling the tickets can be calculated as follows:
- Revenue from A = Number of A tickets × Price of A = 3k × 1000 = 3000k
- Revenue from B = Number of B tickets × Price of B = 2k × 500 = 1000k
- Revenue from C = Number of C tickets × Price of C = 5k × 200 = 1000k
Total Revenue = Revenue from A + Revenue from B + Revenue from C
Total Revenue = 3000k + 1000k + 1000k = 5000k
We know that the total collection from selling the tickets is Rs. 2.5 crore, which is Rs. 2,50,00,000. Therefore, we can set up the equation:
5000k = 2,50,00,000
To find k, we divide both sides of the equation by 5000:
k = 2,50,00,000 / 5000
k = 50,000
Now that we have k, we can find the total number of tickets sold:
Total tickets = A + B + C = 3k + 2k + 5k = 10k
Total tickets = 10 × 50,000 = 5,00,000
The total number of tickets sold is 5,00,000.
Topper's Solved these Questions
Similar Questions
There are 40 passengers in a bus, some with Rs 2.50 tickets and the remaining with Rs 3 tickets. If the total collection from these passengers is Rs 112.50, find the number of Rs 2.50 tickets.
View SolutionA, B, C started a shop by investing Rs. 27.000, Rs. 81,000 and Rs. 72,000 respectively. At the end of one year, B's share of total profit was Rs. 36,000. What was the total profit?
View Solution
Knowledge Check
In a cricket match there are three types of tickets say A B and C each costing Rs. 1000, Rs. 500 and Rs. 200 respectively. The ratio of the tickets sold of categories A B and C is 3:2:5. If the total collection from selling the tickets Is Rs 2.5 crore, find the total number of tickets sold?
A5000B4800C50000D52000A fruit seller sold big, medium and small sized apples for Rs 15, Rs 10 and Rs 5 respectively. The total number of apples sold were in the ratio 3:2:5. Find the average cost of an apple.
A8B10C9D7The fair of 3 full tickets and 2 half tickets is Rs 204 and the fair of 2 full tickets and 3 half tickets is Rs 186. find the fair of a full ticket and a half ticket.
ARs 94BRs 78CRs 86DRs 62
On the first day of the sale of tickets of a drama, in all 35 tickets were sold. If the rates of the tickets were Rs. 20 and Rs. 40 per ticket and the total collection was Rs. 900. Find the number of tickets sold at each rate.
View SolutionFor a journey the cost of a child ticket is 1/3 rd of the cost of an adult ticket. If the cost of the tickets for 4 adults and 5 children is Rs. 85, the cost of a child ticket is :
View SolutionFor a journey the cost of a child ticket is 1/3 rd of the cost of an adult ticket. If the cost of the tickets for 4 adults and 5 children is Rs. 85, the cost of a child ticket is :
View SolutionThe bar graph, given here, shows the number of tickets sold by 6 students A, B, C, D, E and F during a fair. Observe the graph and answer questions based on it.

Total number of tickets sold by A, B and C is
View SolutionThe bar graph, given here, shows the number of tickets sold by 6 students A, B, C, D, E and F during a fair. Observe the graph and answer questions based on it.
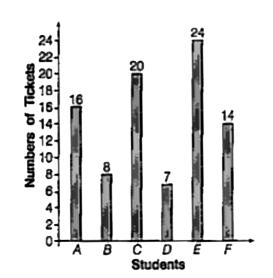
Total number of tickets sold by D, E and F is
View Solution
