If there are two section of class SSC in Mother's Coaching ,section A says if some of students of section B will take transfer and join us then ratio of students of class A to that of class B becometes take transfer of section B then this ratio becomes 4:7 , then among option which can be a value of number of tranfers .
97
47
87
Not possible
To solve the problem step by step, we need to analyze the information given and derive the necessary equations based on the ratios provided.
Step 1: Define Variables
Let:
- a = number of students in Section A
- b = number of students in Section B
- x = number of students transferring from Section B to Section A
Step 2: Set Up the Ratio
According to the problem, after x students transfer from Section B to Section A, the new number of students in Section A will be a+x and in Section B will be b−x. The ratio of students in Section A to Section B then becomes:
a+xb−x=47
Step 3: Cross-Multiply to Eliminate the Fraction
Cross-multiplying gives us:
7(a+x)=4(b−x)
Step 4: Expand and Rearrange the Equation
Expanding both sides:
7a+7x=4b−4x
Now, rearranging the equation to isolate terms involving x:
7a+7x+4x=4b
7a+11x=4b
Step 5: Solve for x
Now, we can express x in terms of a and b:
11x=4b−7a
x=4b−7a11
Step 6: Analyze the Result
For x to be a valid number of students (a non-negative integer), 4b−7a must be divisible by 11.
Step 7: Conclusion
Since we do not have specific values for a and b, we cannot determine a specific value for x. However, we can conclude that the problem states that one of the options is "not possible," which suggests that there are values of a and b for which 4b−7a cannot be divisible by 11.
Final Answer
Thus, the answer to the question is that one of the options given is "not possible."
---
Let:
- a = number of students in Section A
- b = number of students in Section B
- x = number of students transferring from Section B to Section A
According to the problem, after x students transfer from Section B to Section A, the new number of students in Section A will be a+x and in Section B will be b−x. The ratio of students in Section A to Section B then becomes:
a+xb−x=47
Cross-multiplying gives us:
7(a+x)=4(b−x)
Expanding both sides:
7a+7x=4b−4x
Now, rearranging the equation to isolate terms involving x:
7a+7x+4x=4b
7a+11x=4b
Now, we can express x in terms of a and b:
11x=4b−7a
x=4b−7a11
For x to be a valid number of students (a non-negative integer), 4b−7a must be divisible by 11.
Since we do not have specific values for a and b, we cannot determine a specific value for x. However, we can conclude that the problem states that one of the options is "not possible," which suggests that there are values of a and b for which 4b−7a cannot be divisible by 11.
Thus, the answer to the question is that one of the options given is "not possible."
Topper's Solved these Questions
Similar Questions
If there are two sections of class SSC in Mother 's Coaching , section A says if some of students of section B will join us then ratio of students of class A to that of class B becomes 4:9 , but if some of our classmates goes to section B then according to govt .rule one school can take max 200 students in one class (in cluding all sections) then total number of studets in class SSC.
View SolutionThe ratio of the number of students of three class is 2:3:5 .If 20 students are added in each class then the ratio becomes 4:5:7.Find the number of student in each class before adding .
View Solution
Knowledge Check
A class is divided into two sections A and B . Passing average of 20 students of section A is 80% and passing average of 30 students of section B is 70% . What is the passing average of both the sections ?
A0.72B0.74C0.75D0.77Let there are 4 sections of 25 students each in a coaching class. Now, out of 150 students 100 are to be selected randomly and entrolled in these sections. Then, the probability that the students A and B (both present in 150 students) are selected and placed in the same section, is
A1013B16149C233D5149Out of two sections A and B, 10 students of section B shift to A, as a result strength of A becomes 3 times the strength of B. But, if 10 students shift over from A to B, both A and B become equal in strength. Ratio of the number of students in section A that of section B is
A2:1B5:3C3:1D9:4
In a school there are two sections, namely A and B, of class X. there are 30 students in section A and 28 students in section B. find the minimum number of books required for their class library so that they can be distributed equally among students of section A ore section B.
View SolutionIn a school there are two sections section A and section B of class X . There are 32 students in section A and 36 students in section B . Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B .
View SolutionIn a school there are two sections- section A and section B of classX, There are 32 students in section A. 36 students in section B. Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B
View SolutionIn a school, there are five sections of Class VI. The number of students in each section is given below:
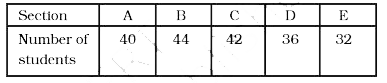
Represent the above data using a bar graph.
View SolutionThe total number of students in section A and B of a class is 110. The number of students in section A is 10 more than that of section B. The average score of the students in B, in a test, is 20% more than that of students in A. If the average score of all the students in the class is 72, then what is the average score of the students in A?
किसी कक्षा के खंड A और खंड B के छात्रों की कुल संख्या 110 है | खंड A में छात्रों की संख्या खंड 9 के छात्रों की संख्या से 10 अधिक है| किसी परीक्षा में B के छात्रों का औसत प्राप्तंक A के छात्रों के औसत प्राप्तंक से 20% अधिक है | यदि सभी छात्रों का औसत प्राप्तांक 72 है, तो A के छात्रों का औसत प्राप्तांक ज्ञात करें |
View Solution