When (43101+23101) is divided by 66, then the remainder will be?
1
2
3
0
The correct Answer is:d
To find the remainder when 43101+23101 is divided by 66, we can use properties of modular arithmetic.
1. Identify the Expression: We need to evaluate 43101+23101mod66.
2. Use the Chinese Remainder Theorem: Since 66 can be factored into 2×3×11, we will find 43101+23101 modulo 2, 3, and 11 separately.
3. Calculate mod2:
- 43≡1mod2
- 23≡1mod2
- Therefore, 43101+23101≡1101+1101≡1+1≡0mod2.
4. Calculate mod3:
- 43≡1mod3
- 23≡2mod3
- Therefore, 43101+23101≡1101+2101≡1+2≡0mod3.
5. Calculate mod11:
- 43≡10mod11
- 23≡1mod11
- Therefore, 43101+23101≡10101+1101.
- By Fermat's Little Theorem, 1010≡1mod11, so 10101=(1010)10⋅101≡110⋅10≡10mod11.
- Thus, 10101+1101≡10+1≡11≡0mod11.
6. Combine Results Using CRT:
- We have:
- 43101+23101≡0mod2
- 43101+23101≡0mod3
- 43101+23101≡0mod11
- Since the results are all 0, we conclude that 43101+23101≡0mod66.
7. Final Result: The remainder when 43101+23101 is divided by 66 is 0.
- 43≡1mod2
- 23≡1mod2
- Therefore, 43101+23101≡1101+1101≡1+1≡0mod2.
- 43≡1mod3
- 23≡2mod3
- Therefore, 43101+23101≡1101+2101≡1+2≡0mod3.
- 43≡10mod11
- 23≡1mod11
- Therefore, 43101+23101≡10101+1101.
- By Fermat's Little Theorem, 1010≡1mod11, so 10101=(1010)10⋅101≡110⋅10≡10mod11.
- Thus, 10101+1101≡10+1≡11≡0mod11.
- We have:
- 43101+23101≡0mod2
- 43101+23101≡0mod3
- 43101+23101≡0mod11
- Since the results are all 0, we conclude that 43101+23101≡0mod66.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
When
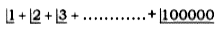 is divided by 8 then the remainder will be? A2B3C1D4
is divided by 8 then the remainder will be? A2B3C1D4 - Question 2 - Select One
When
 is divided by 12 then the remainder will be? A9B8C7D6
is divided by 12 then the remainder will be? A9B8C7D6 - Question 3 - Select One
If the number 2332−9 is divided by 16, then the remainder is :
A8B0C6Dnone of these
If 3101−2100 is divided by 11, the remainder is
View SolutionWhen (43×83) is divided by 21, the remainder obtained is ?
View SolutionIf the number 2332−9 is divided by 16, then the remainder is :
View SolutionWhen 3010301 is divided by 43, the quotient is
View SolutionWhen 721+722+723+724 is divided by 25 the remainder is :
View Solution

