Find tHe correct value upto 5 places of decimal of 1−120+1202−1203+...
1.05
0.95238
0.95239
10.5
The correct Answer is:a
To find the value of the series S=1−120+1202−1203+…, we can recognize that this is an infinite geometric series.
Step 1: Identify the first term and common ratio
The first term a of the series is 1 and the common ratio r is −120.
Step 2: Use the formula for the sum of an infinite geometric series
The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
where |r|<1.
Step 3: Substitute the values into the formula
Substituting the values of a and r:
S=11−(−120)=11+120=12120=2021
Step 4: Convert the fraction to decimal
Now, we need to convert 2021 into a decimal. We can do this by performing the division:
20÷21≈0.95238095238…
Step 5: Round to 5 decimal places
Rounding 0.95238095238 to 5 decimal places gives us:
0.95238
Final Answer
Thus, the correct value of the series up to 5 decimal places is:
0.95238
The first term a of the series is 1 and the common ratio r is −120.
The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
where |r|<1.
Substituting the values of a and r:
S=11−(−120)=11+120=12120=2021
Now, we need to convert 2021 into a decimal. We can do this by performing the division:
20÷21≈0.95238095238…
Rounding 0.95238095238 to 5 decimal places gives us:
0.95238
Thus, the correct value of the series up to 5 decimal places is:
0.95238
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the value of 2×√3 upto three places of decimal.
A1.732B3.464C4.64D2.732 - Question 2 - Select One
Find the value of :20% of 1 hour
AA) 10 minutesBB) 20 minutesCC) 30 minutesDD) 40 minutes
Evaluate (1003)1/3 upto five places of decimal.
View SolutionFind the value of e, correct to 3 decimal places
e=1+12!+13!+14!...View Solution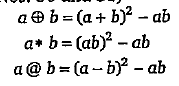
Find the value of (((1⊕2)*3)@20)View SolutionEvaluate (1001)13 upto six places of decimal.
View SolutionThe value of √2 upto three places of decimal is (a) 1.410 (b) 1.412 (c) 1.413 (d) 1.414
View SolutionEvaluate (1.056)1/3 correct up to the four places of decimal.
View Solution

