What is the value of [11−x(q−p)+11−x(p−q)] ?
0
1
(xq−xp)/(xq+xp)
(xq+xp)/(xq−p)
The correct Answer is:B
To solve the expression 11−x(q−p)+11−x(p−q), we will follow these steps:
Step 1: Rewrite the expression
The expression can be rewritten using the property of exponents:
11−x(q−p)+11−x(p−q)
Notice that x(p−q) can be rewritten as xpxq and x(q−p) can be rewritten as xqxp.
Step 2: Substitute the rewritten exponents
Substituting these into the expression gives:
11−xqxp+11−xpxq
Step 3: Simplify each term
Now we simplify each term:
1. The first term becomes:
1xp−xqxp=xpxp−xq
2. The second term becomes:
1xq−xpxq=xqxq−xp
Step 4: Combine the fractions
Now we can combine the two fractions:
xpxp−xq+xqxq−xp
Notice that xq−xp=−(xp−xq), so we can rewrite the second term:
xpxp−xq−xqxp−xq
Step 5: Combine the numerators
Now, combine the numerators over the common denominator:
xp−xqxp−xq
Step 6: Simplify the expression
Since the numerator and denominator are the same, we have:
1
Final Answer:
The value of the expression is:
1
The expression can be rewritten using the property of exponents:
11−x(q−p)+11−x(p−q)
Notice that x(p−q) can be rewritten as xpxq and x(q−p) can be rewritten as xqxp.
Substituting these into the expression gives:
11−xqxp+11−xpxq
Now we simplify each term:
1. The first term becomes:
1xp−xqxp=xpxp−xq
2. The second term becomes:
1xq−xpxq=xqxq−xp
Now we can combine the two fractions:
xpxp−xq+xqxq−xp
Notice that xq−xp=−(xp−xq), so we can rewrite the second term:
xpxp−xq−xqxp−xq
Now, combine the numerators over the common denominator:
xp−xqxp−xq
Since the numerator and denominator are the same, we have:
1
The value of the expression is:
1
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
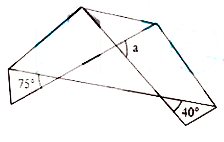
What is the value of a?A65∘B75∘C105∘D115∘ - Question 2 - Select One
What is the value of B?
A815B1615C3215D0 - Question 3 - Select One
What is the value of I1
A2πBπCπ/2D2π

