Question

A person is standing on weighing machine and is slowly taken from the surface of earth to the surface of mars.Given that the value of g on earth is $10m{s}^{-2}$ and that on Mars is $4m{s}^{-2}$.Draw graph of weight vs distance from earth's surface

Options

A.
B.
C.
D.

Explanation

To solve the problem of drawing a graph of weight versus distance from the Earth's surface as a person is taken to the surface of Mars, we can follow these steps:

1. Understanding Weight on Earth:
- The weight of the person on Earth can be calculated using the formula:
\( W_0 = m \cdot g_e \)
- Given that \( g_e = 10 \, \text{m/s}^2 \), we can express the weight as:
\( W_0 = m \cdot 10 \)

2. Understanding Weight on Mars:
- The weight of the person on Mars is given by:
\( W' = m \cdot g_m \)
- Given that \( g_m = 4 \, \text{m/s}^2 \), we can express the weight on Mars as:
\( W' = m \cdot 4 \)

3. Finding Mass:
- We can express the mass \( m \) in terms of \( W_0 \):
\( m = \frac{W_0}{10} \)

4. Weight on Mars in Terms of \( W_0 \):
- Substituting the expression for mass into the weight on Mars, we get:
\( W' = \left(\frac{W_0}{10}\right) \cdot 4 = \frac{4W_0}{10} = 0.4W_0 \)

5. Weight Variation with Distance:
- As the person is taken from the Earth's surface to Mars, the weight will change due to the varying gravitational effects. The weight will decrease from \( W_0 \) to \( 0.4W_0 \) as the person moves away from Earth and approaches Mars.
- There will be a point where the gravitational pull from Earth and Mars will balance each other, resulting in zero weight. This point can be found by setting the gravitational forces equal.

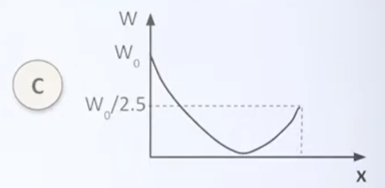
6. Graphing Weight vs. Distance:
- The graph will start at \( W_0 \) when the person is on Earth.
- As the distance from the Earth's surface increases, the weight will decrease non-linearly (due to the inverse square law of gravitation).
- The graph will reach zero weight at a certain distance where the gravitational pull from Mars equals that of Earth.
- After this point, as the person moves closer to Mars, the weight will stabilize at \( 0.4W_0 \).

Graph Description:
- The x-axis represents the distance from the Earth's surface.
- The y-axis represents the weight of the person.
- The graph starts at \( W_0 \) and curves downwards, crossing the x-axis (weight = 0) at a certain point, and then continues to approach \( 0.4W_0 \) as the distance increases towards Mars.