A uniform rod of young's modulus Y is tretched by two tension $T_{1}$ and $T_{2}$ such that rods gets expanded to length $L_{1}$ and $L_{2}$ respectively.Find initial length of rod?

$\frac{L_{1} T_{1} - L_{2} T_{2}}{T_{1} - T_{2}}$

$\frac{L_{2} T_{1} - L_{1} T_{2}}{T_{2} - T_{1}}$

$\frac{L_{1} T_{2} - L_{2} T_{1}}{T_{2} - T_{1}}$

$\frac{L_{1}}{T_{1}} \cdot \frac{T_{2}}{T_{2}}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the initial length of a uniform rod that is stretched by two different tensions, we can follow these steps:
1. Define Variables:
- Let the initial length of the rod be $L$ .
- When tension $T_{1}$ is applied, the rod expands to length $L_{1}$ .
- When tension $T_{2}$ is applied, the rod expands to length $L_{2}$ .
- The increase in length due to tension $T_{1}$ is $Δ L_{1} = L_{1} - L$ .
- The increase in length due to tension $T_{2}$ is $Δ L_{2} = L_{2} - L$ .
2. Use Young's Modulus:
- Young's modulus $Y$ is defined as:
$Y = \frac{Stress}{Strain}$
- Stress is given by $\frac{T}{A}$ (where $T$ is tension and $A$ is the cross-sectional area), and strain is given by $\frac{Δ L}{L}$ .
3. Set Up Equations:
- For tension $T_{1}$ :
$Y = \frac{T_{1} / A}{(L_{1} - L) / L} ⟹ Y = \frac{T_{1} L}{A (L_{1} - L)}$
- For tension $T_{2}$ :
$Y = \frac{T_{2} / A}{(L_{2} - L) / L} ⟹ Y = \frac{T_{2} L}{A (L_{2} - L)}$
4. Equate Young's Modulus:
- Since both expressions for Young's modulus are equal:
$\frac{T_{1} L}{A (L_{1} - L)} = \frac{T_{2} L}{A (L_{2} - L)}$
- The area $A$ cancels out:
$\frac{T_{1} L}{L_{1} - L} = \frac{T_{2} L}{L_{2} - L}$
5. Cross-Multiply:
- Cross-multiplying gives:
$T_{1} (L_{2} - L) = T_{2} (L_{1} - L)$
6. Rearrange the Equation:
- Rearranging the equation leads to:
$T_{1} L_{2} - T_{1} L = T_{2} L_{1} - T_{2} L$
- Bringing like terms together:
$T_{1} L_{2} - T_{2} L_{1} = (T_{1} - T_{2}) L$
7. Solve for Initial Length $L$ :
- Finally, we can solve for $L$ :
$L = \frac{T_{1} L_{2} - T_{2} L_{1}}{T_{1} - T_{2}}$
Final Answer:
$L = \frac{T_{1} L_{2} - T_{2} L_{1}}{T_{1} - T_{2}}$

The Young's modulus of a wire of length L and radius r is Y. If the length and radius is reduced to L/2 and r/2 respectively, then its Young' modulus will be
A $Y / 2$
BY
C2Y
D4Y
A uniform rod of length $L$ (in between the supports) and mass $m$ is placed on two support $A$ and $B$ . The rod breaks suddenly at length $L / 10$ from the support $B$ . Find the reaction at support $A$ immediately after the rod breaks

A $\frac{9}{40} m g$
B $\frac{19}{40} m g$
C $\frac{m g}{2}$
D $\frac{9}{20} m g$
One end of a thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two sections of length $l_{1} and l_{2}$ and thermal conductivities $K_{1} and K_{2}$ respectively. The temperature at the interface of the two section is

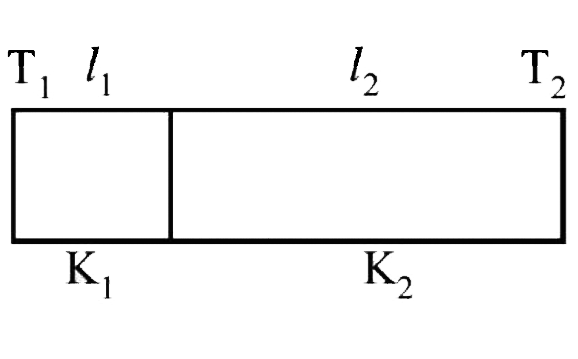A $\frac{K_{1} l_{1} T_{1} + K_{2} l_{2} T_{2}}{K_{1} l_{1} + K_{2} l_{2}}$
B $\frac{K_{2} l_{2} T_{1} + K_{1} l_{1} T_{2}}{K_{1} l_{1} + K_{2} l_{2}}$
C $\frac{K_{2} l_{1} T_{1} + K_{1} l_{2} T_{2}}{K_{2} l_{1} + K_{1} l_{2}}$
D $\frac{K_{1} l_{2} T_{1} + K_{2} l_{1} T_{2}}{K_{1} l_{2} + K_{2} l_{1}}$