Are the following sets of ordered pairs functions ? If so, examine whether the mapping is surjective or injective :
{(a, b) : a is a person, b is an ancestor of a}
The correct Answer is:It is not a function
To determine whether the set of ordered pairs {(a,b):a is a person, b is an ancestor of a} represents a function, we need to analyze the definition of a function and the nature of the relationship between the elements a and b.
1. Definition of a Function:
A set of ordered pairs is considered a function if each element in the domain (the first component of the pairs) is associated with exactly one element in the codomain (the second component of the pairs).
2. Identify the Domain and Codomain:
In this case, the domain consists of all persons a, and the codomain consists of all possible ancestors b of those persons.
3. Examine the Relationship:
For a given person a, there can be multiple ancestors b. For example, a person can have a mother, father, grandparents, etc. This means that for a single input a, there are multiple possible outputs b.
4. Conclusion on Functionality:
Since a single person a can be associated with multiple ancestors b, this violates the definition of a function, which requires that each input has a unique output. Therefore, the set of ordered pairs does not represent a function.
5. Surjectivity and Injectivity:
Since the set is not a function, we cannot examine whether it is surjective (onto) or injective (one-to-one). These properties only apply to sets that qualify as functions.
Final Answer:
The set {(a,b):a is a person, b is an ancestor of a} is not a function because a single person can have multiple ancestors, leading to multiple outputs for a single input.
A set of ordered pairs is considered a function if each element in the domain (the first component of the pairs) is associated with exactly one element in the codomain (the second component of the pairs).
In this case, the domain consists of all persons a, and the codomain consists of all possible ancestors b of those persons.
For a given person a, there can be multiple ancestors b. For example, a person can have a mother, father, grandparents, etc. This means that for a single input a, there are multiple possible outputs b.
Since a single person a can be associated with multiple ancestors b, this violates the definition of a function, which requires that each input has a unique output. Therefore, the set of ordered pairs does not represent a function.
Since the set is not a function, we cannot examine whether it is surjective (onto) or injective (one-to-one). These properties only apply to sets that qualify as functions.
The set {(a,b):a is a person, b is an ancestor of a} is not a function because a single person can have multiple ancestors, leading to multiple outputs for a single input.
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test13videos
CONCEPTS OF SET THEORY
- BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Problem Set (2) (RELATIONS)47videos
CONCEPTS OF SET THEORY
- BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Assertion / Reason2videos
COMPLEX NUMBERS
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - SELF ASSESSMENT TEST10videos
CORRELATION AND REGRESSION
Similar Questions
Are the following sets of ordered pairs functions? If so, examine whether the mapping is surjective or injective:
{(x, y):x is a person, y is the mother of x}View SolutionAre the following sets of ordered pairs functions? If so, examine whether the mapping is surjective or injective:
{(x, y):x is a person, y is the mother of x}View Solution
Knowledge Check
- Question 1 - Select One
Which of the following function is surjective but not injective?
Af:R→R,f(x)=x4+2x3−x2+1Bf:R→R,f(x)=x3+x+1Cf:R→R+,f(x)=√1+x2Df:R→R,f(x)=x3+2x2−x+1 - Question 2 - Select One
Which of the following function is surjective but not injective?
Af:R→R,f(x)=x4+2x3−x2+1Bf:R→R,f(x)=x3+x+1Cf:R→R,f(x)=√1+x2Df:R→R,f(x)=x3+2x2−x+1 - Question 3 - Select One
The function f:A→B, defined by a mapping below, is:
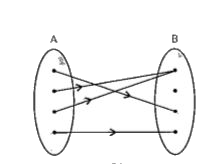 Aone-oneBontoCintoDbijective
Aone-oneBontoCintoDbijective
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective: {(x, y):x is a person, y is the mother of x} (ii) {(a, b):a is a person, b is an ancestor of a}
View SolutionExamine whether the following statements are true or false :
{a,b}⊂{b,c,a}View SolutionExamine whether the binary operation ∗ defined on R by a∗b=ab+1 is associative or not.
View SolutionIn Fig. 5.63, examine whether the following pairs of lines are parallel or not:
(i) EF and GH (ii) AB and CD
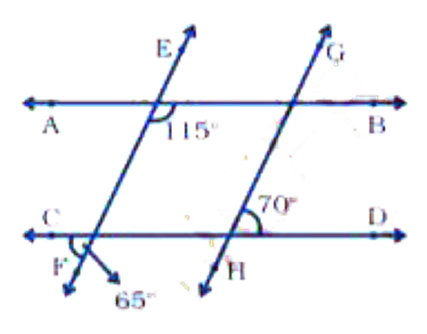 View Solution
View SolutionWhich of the following pairs of months is used in Isothermal maps to examine extremes of temperature.
View Solution

