The digit at unit place in the number 171995+111995−71995 is
0
1
2
3
The correct Answer is:b
To find the digit at the unit place in the expression 171995+111995−71995, we will analyze the unit digits of each term separately.
Step 1: Find the unit digit of 171995
The unit digit of 171995 is the same as the unit digit of 71995 because the unit digit of a number only depends on the unit digit of the base.
To determine the unit digit of 71995, we observe the pattern in the unit digits of powers of 7:
- 71=7 (unit digit is 7)
- 72=49 (unit digit is 9)
- 73=343 (unit digit is 3)
- 74=2401 (unit digit is 1)
- 75=16807 (unit digit is 7)
The unit digits repeat every 4 terms: 7,9,3,1.
To find 71995, we calculate 1995mod4:
1995÷4=498remainder 3
Thus, 1995mod4=3. Therefore, the unit digit of 71995 corresponds to the unit digit of 73, which is 3.
Step 2: Find the unit digit of 111995
The unit digit of 111995 is the same as the unit digit of 11995 since the unit digit of 11 is 1.
The unit digit of 11995 is always 1.
Step 3: Combine the unit digits
Now we can combine the unit digits we found:
- Unit digit of 171995 (which is the same as 71995): 3
- Unit digit of 111995: 1
- Unit digit of 71995: 3
Now we calculate:
Unit digit of (171995+111995−71995)=(3+1−3)
Calculating this gives:
3+1=4and then4−3=1
Final Answer
The digit at the unit place in the number 171995+111995−71995 is 1.
---
The unit digit of 171995 is the same as the unit digit of 71995 because the unit digit of a number only depends on the unit digit of the base.
- 71=7 (unit digit is 7)
- 72=49 (unit digit is 9)
- 73=343 (unit digit is 3)
- 74=2401 (unit digit is 1)
- 75=16807 (unit digit is 7)
1995÷4=498remainder 3
Thus, 1995mod4=3. Therefore, the unit digit of 71995 corresponds to the unit digit of 73, which is 3.
The unit digit of 111995 is the same as the unit digit of 11995 since the unit digit of 11 is 1.
Now we can combine the unit digits we found:
- Unit digit of 171995 (which is the same as 71995): 3
- Unit digit of 111995: 1
- Unit digit of 71995: 3
Unit digit of (171995+111995−71995)=(3+1−3)
Calculating this gives:
3+1=4and then4−3=1
The digit at the unit place in the number 171995+111995−71995 is 1.
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - BINOMIAL THEOREM AND MATHEMATICAL INDUCTION EXERCISE - Problem Set (1) (TRUE AND FALSE)4videos
BINOMIAL THEOREM AND MATHEMATICAL INDUCTION
- BOOK - ML KHANNACHAPTER - BINOMIAL THEOREM AND MATHEMATICAL INDUCTION EXERCISE - Problem Set (1) (FILL IN THE BLANKS)3videos
BINOMIAL THEOREM AND MATHEMATICAL INDUCTION
- BOOK - ML KHANNACHAPTER - AREA OF CURVESEXERCISE - SELF ASSESSEMENT TEST16videos
AREA OF CURVES
- BOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - SELF ASSIGNMENT TEST11videos
CO-ORDINATE GEOMETRY OF THREE DIMENSION
Similar Questions
Knowledge Check
- Question 1 - Select One
The digit in unit's place of the number (1570)2+(1571)2+(1572)2+(1573)2 is:
A0B4C6D8 - Question 2 - Select One
The digit at the unit place in the number 192005+112005−92005 is :
A2B1C0D8 - Question 3 - Select One
Find out the unit digit in the -
(17)1999+(11)1999−(7)1999A0B1C2D7
What is the unit place digit in the expansion of 773 ?
View Solution(2005)^(2)-(1995)^(2)=?
View Solution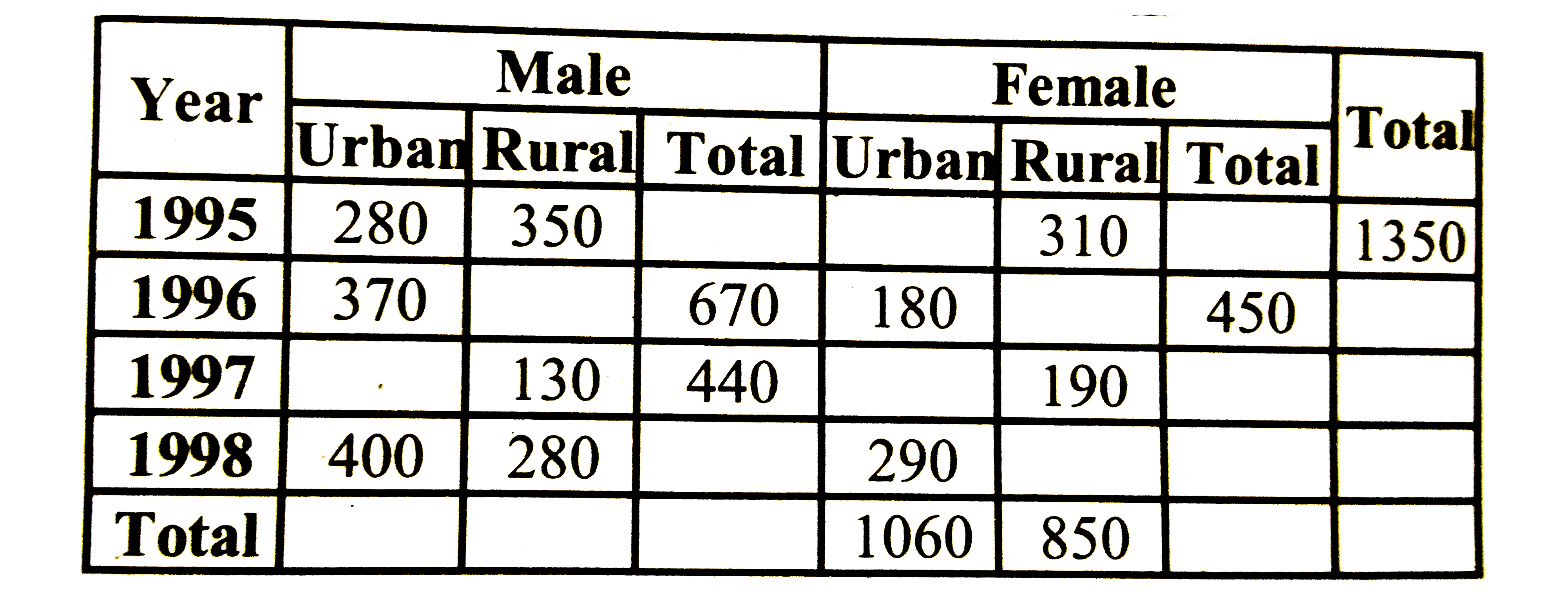
What is the female urban population in the year 1995?View SolutionThe digit in the units place of the number represented by (795−358) is:
View SolutionThe units digit of 172009+112009−72009 is
View Solution

