∣∣ ∣ ∣ ∣∣1aa2a3+bcd1bb2b3+cda1cc2c3+abd1dd2d3+abc∣∣ ∣ ∣ ∣∣ =
a3b3c3
b3c3d3
c3d3a3
0
The correct Answer is:D
To solve the determinant
D=∣∣
∣
∣
∣∣1aa2a3+bcd1bb2b3+cda1cc2c3+abd1dd2d3+abc∣∣
∣
∣
∣∣
we can use properties of determinants to simplify the calculation.
Step 1: Split the determinant
We can split the last column into two parts:
D=∣∣
∣
∣
∣∣1aa2a31bb2b31cc2c31dd2d3∣∣
∣
∣
∣∣+∣∣
∣
∣
∣∣1aa2bcd1bb2cda1cc2abd1dd2abc∣∣
∣
∣
∣∣
Let's denote the first determinant as D1 and the second as D2.
Step 2: Evaluate D1
The determinant D1 is a Vandermonde determinant, which can be calculated as:
D1=(b−a)(c−a)(d−a)(c−b)(d−b)(d−c)
Step 3: Evaluate D2
Now, we will evaluate D2. Notice that we can factor out bcd, cda, abd, and abc from the last column.
We can express D2 as:
D2=∣∣
∣
∣
∣∣1aa201bb201cc201dd20∣∣
∣
∣
∣∣+∣∣
∣
∣
∣∣1aa2bcd1bb2cda1cc2abd1dd2abc∣∣
∣
∣
∣∣
The first part is clearly zero since the last column is all zeros. Therefore, D2 simplifies to:
D2=∣∣
∣
∣
∣∣1aa2bcd1bb2cda1cc2abd1dd2abc∣∣
∣
∣
∣∣
Step 4: Combine D1 and D2
Now, we can combine D1 and D2:
D=D1+D2
Step 5: Final evaluation
Since D1 is non-zero (as long as a, b, c, and d are distinct), and D2 can be shown to be zero due to the properties of determinants (as the last column can be expressed as a linear combination of the other columns), we conclude that:
D=D1+0=D1
Thus, the final value of the determinant D is:
D=0
∣
∣
∣∣1aa2a3+bcd1bb2b3+cda1cc2c3+abd1dd2d3+abc∣∣
∣
∣
∣∣
We can split the last column into two parts:
∣
∣
∣∣1aa2a31bb2b31cc2c31dd2d3∣∣
∣
∣
∣∣+∣∣
∣
∣
∣∣1aa2bcd1bb2cda1cc2abd1dd2abc∣∣
∣
∣
∣∣
The determinant D1 is a Vandermonde determinant, which can be calculated as:
Now, we will evaluate D2. Notice that we can factor out bcd, cda, abd, and abc from the last column.
∣
∣
∣∣1aa201bb201cc201dd20∣∣
∣
∣
∣∣+∣∣
∣
∣
∣∣1aa2bcd1bb2cda1cc2abd1dd2abc∣∣
∣
∣
∣∣
∣
∣
∣∣1aa2bcd1bb2cda1cc2abd1dd2abc∣∣
∣
∣
∣∣
Now, we can combine D1 and D2:
Since D1 is non-zero (as long as a, b, c, and d are distinct), and D2 can be shown to be zero due to the properties of determinants (as the last column can be expressed as a linear combination of the other columns), we conclude that:
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - DETERMINANTS EXERCISE - Problem Set (1) (TRUE AND FALSE)7videos
DETERMINANTS
- BOOK - ML KHANNACHAPTER - DETERMINANTS EXERCISE - Problem Set (2) (MULTIPLE CHOICE QUESTIONS)21videos
DETERMINANTS
- BOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - Miscellaneous Questions (Assertion/Reason)1videos
DEFINITE INTEGRAL
- BOOK - ML KHANNACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - MISCELLANEOUS EXERCISE (Matching Entries)2videos
DIFFERENTIAL EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If A=∣∣ ∣ ∣∣111abca3b3c3∣∣ ∣ ∣∣,B=∣∣ ∣ ∣∣111a2b2c2a3b3c3∣∣ ∣ ∣∣,C=∣∣ ∣ ∣∣abca2b2c2a3b3c3∣∣ ∣ ∣∣ , then which relation is correct :
AA=BBA=CCB=CDNone of these - Question 2 - Select One
If a=a1i+a2j+a3k,b=b1i+b2j+b3k,c=c1i+c2j+c3k,d=d1i+d2j+d3k and
k(a×b)×(c×d)=∣∣ ∣ ∣ ∣∣−a−bcda1b1c1d1a2b2c2d2a3b3c3d3∣∣ ∣ ∣ ∣∣
(formal expression) thenAk = 16Bk = 2Ck = 4Dnone of these - Question 3 - Select One
If a1x3+b1x2+c1x+d1=0anda2x3+b2x2+c2x+d2=0 have a pair of common positive repeated roots. If the value of ∣∣ ∣ ∣ ∣∣3a12b1c13a22b2c2a2b1−a1b2c1a2−c2a1d1a2−a2d2∣∣ ∣ ∣ ∣∣ is
A3B2C1D0
If ∣∣ ∣ ∣∣aa21+a3bb21+b3cc21+c2∣∣ ∣ ∣∣=0 and vectors (1,a,a2),(1,b,b2)and(1,c,c2) are hon coplanar then the product abc equals (A) 2 (B) -1 (C) 1 (D) 0
View Solution∣∣ ∣ ∣∣aa2a3−1bb2b3−1cc2c3−1∣∣ ∣ ∣∣=0 prove that abc=I
View SolutionIf a2+b2+c2+ab+bc+ca≤0∀a,b,c∈R then find the value of the determinant ∣∣ ∣ ∣∣(a+b+2)2a2+b211(b+c+2)2b2+c2c2+a21(c+a+2)2∣∣ ∣ ∣∣ : (A) abc(a2+b2+c2) (B) 0 (C) a3+b3+c3+3abc (D) 65
View SolutionMatch the following:
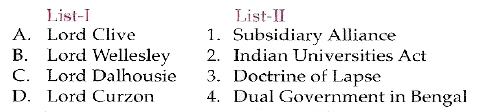
(a) ABCD2341 (b) ABCD4132
(c) ABCD4321 (d) ABCD1423View Solutionif D1=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣ and D2=∣∣ ∣∣a1+2a2+3a32a35a2b1+2b2+3b32b35b2c1+2c2+3c32c35c2∣∣ ∣∣ then D2D1 is equal to :
View Solution

