Assuming that the sums and products given below are defined which of the following is not true for matrices.
AB=AC does not imply B=C
A+B=B+A
(AB)'=B'A'
AB=O⇒A=O or B=O
The correct Answer is:D
To determine which of the given statements about matrices is not true, we will analyze each option step by step.
Step 1: Define the Matrices
Let's define the matrices as follows:
- Matrix A = (1236)
- Matrix B = (1764)
- Matrix C = (51142)
Step 2: Check Option 1
We need to check if AB=AC implies B=C.
1. Calculate AB:
AB=(1236)(1764)
- First row, first column: 1⋅1+2⋅6=1+12=13
- First row, second column: 1⋅7+2⋅4=7+8=15
- Second row, first column: 3⋅1+6⋅6=3+36=39
- Second row, second column: 3⋅7+6⋅4=21+24=45
Thus,
AB=(13153945)
2. Calculate AC:
AC=(1236)(51142)
- First row, first column: 1⋅5+2⋅4=5+8=13
- First row, second column: 1⋅11+2⋅2=11+4=15
- Second row, first column: 3⋅5+6⋅4=15+24=39
- Second row, second column: 3⋅11+6⋅2=33+12=45
Thus,
AC=(13153945)
Since AB=AC but B≠C, this option is true.
Step 3: Check Option 2
We need to check if A+B=B+A.
1. Calculate A+B:
A+B=(1236)+(1764)=(1+12+73+66+4)=(29910)
2. Calculate B+A:
B+A=(1764)+(1236)=(1+17+26+34+6)=(29910)
Since A+B=B+A, this option is true.
Step 4: Check Option 3
We need to verify if (AB)T=BTAT.
1. Calculate (AB)T:
We already found AB=(13153945).
(AB)T=(13391545)
2. Calculate BT and AT:
BT=(1674),AT=(1326)
3. Calculate BTAT:
BTAT=(1674)(1326)
- First row, first column: 1⋅1+6⋅2=1+12=13
- First row, second column: 1⋅3+6⋅6=3+36=39
- Second row, first column: 7⋅1+4⋅2=7+8=15
- Second row, second column: 7⋅3+4⋅6=21+24=45
Thus,
BTAT=(13391545)
Since (AB)T≠BTAT, this option is false.
Step 5: Check Option 4
We need to check if AB=0 implies A=0 and B=0.
1. Assume A and B:
Let A=(0040) and B=(0010).
2. Calculate AB:
AB=(0040)(0010)=(0000)
Here, AB=0 does not imply that both A and B are zero. Therefore, this option is false.
Conclusion
The option that is not true is Option 4: AB=0 implies A=0 and B=0.
Let's define the matrices as follows:
- Matrix A = (1236)
- Matrix B = (1764)
- Matrix C = (51142)
We need to check if AB=AC implies B=C.
AB=(1236)(1764)
- First row, first column: 1⋅1+2⋅6=1+12=13
- First row, second column: 1⋅7+2⋅4=7+8=15
- Second row, first column: 3⋅1+6⋅6=3+36=39
- Second row, second column: 3⋅7+6⋅4=21+24=45
AB=(13153945)
AC=(1236)(51142)
- First row, first column: 1⋅5+2⋅4=5+8=13
- First row, second column: 1⋅11+2⋅2=11+4=15
- Second row, first column: 3⋅5+6⋅4=15+24=39
- Second row, second column: 3⋅11+6⋅2=33+12=45
AC=(13153945)
We need to check if A+B=B+A.
A+B=(1236)+(1764)=(1+12+73+66+4)=(29910)
B+A=(1764)+(1236)=(1+17+26+34+6)=(29910)
We need to verify if (AB)T=BTAT.
We already found AB=(13153945).
(AB)T=(13391545)
BT=(1674),AT=(1326)
BTAT=(1674)(1326)
- First row, first column: 1⋅1+6⋅2=1+12=13
- First row, second column: 1⋅3+6⋅6=3+36=39
- Second row, first column: 7⋅1+4⋅2=7+8=15
- Second row, second column: 7⋅3+4⋅6=21+24=45
BTAT=(13391545)
We need to check if AB=0 implies A=0 and B=0.
Let A=(0040) and B=(0010).
AB=(0040)(0010)=(0000)
The option that is not true is Option 4: AB=0 implies A=0 and B=0.
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - MATRICESEXERCISE - PROBLEM SET(1) (ASSERTION /REASON)3videos
MATRICES
- BOOK - ML KHANNACHAPTER - MATRICESEXERCISE - PROBLEM SET(1) (TRUE AND FALSE)9videos
MATRICES
- BOOK - ML KHANNACHAPTER - MATRICESEXERCISE - EXAMPLE4videos
MATRICES
- BOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (2) ASSERTION/REASON3videos
MATHEMATICAL REASONING
- BOOK - ML KHANNACHAPTER - MAXIMA AND MINIMA EXERCISE - MISCELANEOUS EXERCISE (COMPREHENSION)3videos
MAXIMA AND MINIMA
Similar Questions
Knowledge Check
- Question 1 - Select One or More
Given
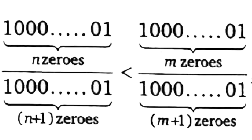
then which of the following trueAm+1<nBm<nCm<n+1Dm>n+1 - Question 2 - Select One
A function f:A→B is defined as :
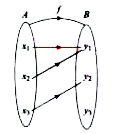
Which of the following is true ?Aone - one functionBone-one and onto functionCmany - one and into functionDmany-one and onto function - Question 3 - Select One
If A and B two are 3×3 matrices then which one of the following is not true:
A(A+B) = A + BB(AB) = A' B'Cdet (AB)= det (A) det (B)DA (adj A) = |A|I3
If A and B are 2×2 matrices, then which of the following is true ?
View SolutionIf A and B are 2×2 matrices, then which of the following is true ?
View SolutionWhich of the following is not true of a pyramid of productivity?
View SolutionWhich of the following is true of net primary production?
View SolutionConsider the reaction sequence given below :
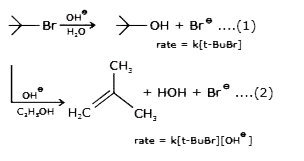
Which of the following statements is true :View Solution

