Which of the following the following is correct?
skew symmetric matrix of even order is always singular
skew symmetric matrix of odd order is non singular
skew symmetric matrix of odd order is singular
None of these
The correct Answer is:A
To determine which of the statements regarding skew-symmetric matrices is correct, let's analyze the properties of skew-symmetric matrices.
Step 1: Definition of Skew-Symmetric Matrix
A matrix A is called skew-symmetric if AT=−A, where AT is the transpose of A.
Step 2: Properties of Determinants
One important property of determinants is that if a matrix is skew-symmetric and of odd order (i.e., the number of rows or columns is odd), then its determinant is zero. This means that such a matrix is singular.
Step 3: Analyzing the Options
1. Option 1: "Skew symmetric matrix of even order is always singular."
- This is not necessarily true. A skew-symmetric matrix of even order can be non-singular.
2. Option 2: "Skew symmetric matrix of odd order is non-singular."
- This is false. As established, a skew-symmetric matrix of odd order is singular (determinant = 0).
3. Option 3: "Skew symmetric matrix of odd order is singular."
- This is true. A skew-symmetric matrix of odd order has a determinant of zero.
4. Option 4: "Skew symmetric matrix of even order is non-singular."
- This is not necessarily true. While some even-order skew-symmetric matrices can be non-singular, others can be singular.
Conclusion
The correct statement is:
- Skew symmetric matrix of odd order is singular.
A matrix A is called skew-symmetric if AT=−A, where AT is the transpose of A.
One important property of determinants is that if a matrix is skew-symmetric and of odd order (i.e., the number of rows or columns is odd), then its determinant is zero. This means that such a matrix is singular.
1. Option 1: "Skew symmetric matrix of even order is always singular."
- This is not necessarily true. A skew-symmetric matrix of even order can be non-singular.
2. Option 2: "Skew symmetric matrix of odd order is non-singular."
- This is false. As established, a skew-symmetric matrix of odd order is singular (determinant = 0).
- This is true. A skew-symmetric matrix of odd order has a determinant of zero.
- This is not necessarily true. While some even-order skew-symmetric matrices can be non-singular, others can be singular.
The correct statement is:
- Skew symmetric matrix of odd order is singular.
Topper's Solved these Questions
- MATRICESBOOK - ML KHANNACHAPTER - MATRICESEXERCISE - PROBLEM SET(1) (ASSERTION /REASON)
3 Videos
- MATRICESBOOK - ML KHANNACHAPTER - MATRICESEXERCISE - PROBLEM SET(1) (TRUE AND FALSE)
9 Videos
- MATRICESBOOK - ML KHANNACHAPTER - MATRICESEXERCISE - EXAMPLE
4 Videos
- MATHEMATICAL REASONINGBOOK - ML KHANNACHAPTER - MATHEMATICAL REASONINGEXERCISE - PROBLEM SET (2) ASSERTION/REASON
3 Videos
- MAXIMA AND MINIMA BOOK - ML KHANNACHAPTER - MAXIMA AND MINIMA EXERCISE - MISCELANEOUS EXERCISE (COMPREHENSION)
3 Videos
Similar Questions
Knowledge Check
Which of the following relationship is correct ?
AΔG∘=−RT In KBK=e−ΔG∘/RTCAll a re correctDall are correctWhich of the following relatiosn is correct ?
AΔS=1T[ΔG−ΔH]BΔV=1P[q+ΔE]CΔHfus=ΔHsub−ΔHvapDΔE=ΔH+ΔnRT.For the following reactions:

Which of the following statement is correct?A(a) is subtstitution, (b) and ( c ) are addition reactionsB(a) and (b)are alimination reaction and (c ) is addition.C(a) is alimination, (b) is substitution and (c ) is addition reactionD(a) iselimination, (b) and ( c) are substitution reaction
For the following reactions : -
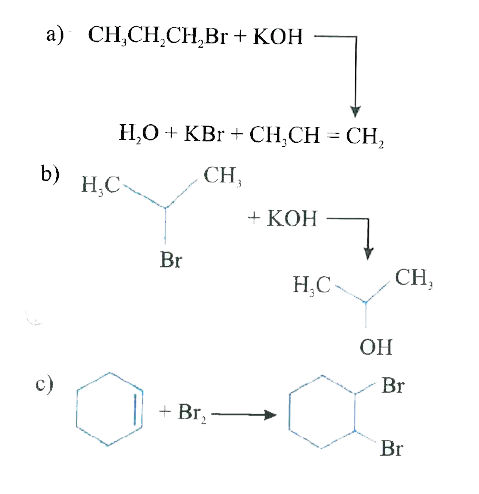
Which of the following statement is correct ?
View SolutionWhich fo the following is not correct?
View SolutionWhich of the following statements is correct?
View Solutionwhich of the following stament is not correct?
View SolutionWhich of the following statements is correct?
View Solution
