Three concurrent lines with direction cosines (l1,m1,n1),(l2,m2,n2)and(l3,m3,n3) are coplanar if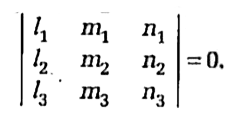 
The correct Answer is:T
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - MISCELLANEOUS EXERCISE( FILL IN THE BLANKS)16videos
CO-ORDINATE GEOMETRY OF THREE DIMENSION
- BOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - MATCHING ENTRIES (MATCH THE ENTERIES OF COLUMN-II WITH THOSE OF COLUMN-II UNDER THE FOLLOWING CONDITIONS : )4videos
CO-ORDINATE GEOMETRY OF THREE DIMENSION
- BOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - PROBLEM SET (4)19videos
CO-ORDINATE GEOMETRY OF THREE DIMENSION
- BOOK - ML KHANNACHAPTER - BINOMIAL THEOREM AND MATHEMATICAL INDUCTION EXERCISE - Self Assessment Test35videos
BINOMIAL THEOREM AND MATHEMATICAL INDUCTION
- BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Assertion / Reason2videos
COMPLEX NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
The direction cosines of a line equally inclined to three mutually perpendiclar lines having direction cosines as l1,m1,n1,l2,m2,n2 and l3,m3,n3 are
Al1+l2+l3,m1+m2+m3,n1+n2+n3Bl1+l2+l3√3,m1+m2+m3√3,n1+n2+n3√3Cl1+l2+l33,m1+m2+m33,n1+n2+n33Dnone of these - Question 2 - Select One
Two lines with direction cosines l1,m1,n1andl2,m2,n2 are at right angle of
Al1l2−m1m2−n1n2=0Bl1l2+m1m2+n1n2=0Cl2=l2,m1=m2,n1=n2Dl1l2=m1m2=n1n2
If three mutually perpendicular lines have direction cosines (l1,m1,n1),(l2,m2,n2)and(L3,m3,n3), then the line having direction cosines l1+l2+l3,m1+m2+m3,andn1+n2+n3, make an angle of
View SolutionThe direction cosines of a line equally inclined to three mutually perpendiclar lines having direction cosines as l1,m1,n1,l2,m2,n2 and l3,m3,n3 are
View SolutionIf A =⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ then Find A+I
View SolutionIf three mutually perpendicular lines have direction cosines (l1,m1,n1),(l2,m2,n2)and(l3,m3,n3), then the line having direction ratio l1+l2+l3,m1+m2+m3,andn1+n2+n3, make an angle of
View SolutionProve that the three lines from O with direction cosines l1,m1,n1:l2,m2,n2:l3,m3,n3 are coplanar, if l1(m2n3−n2m3)+m1(n2l3−l2n3)+n1(l2m3−l3m2)=0
View SolutionProve that the three lines from O with direction cosines l1,m1,n1:l2,m2,n2:l3,m3,n3 are coplanar, if l1(m2n3−n2m3)+m1(n2l3−l2n3)+n1(l2m3−l3m2)=0
View Solution