Let $b = 6$ with a and c satisfying (1). If $α$ and $β$ are the roots of the quadeatic equation $a x^{2} + b x + c = 0, t h e n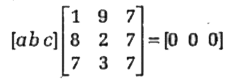$ is

$\frac{6}{7}$

$\infty$

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

If $sin θ$ and $cos θ$ are roots of equation $a x^{2} + b x + c = 0$ , then
Arational numbers
Breal and negative
Cnegative real parts
Dnone of these
If $α$ and $β$ are the roots of the , quadratic equation , $a x^{2} + b x + c = 0$ ,with $α < β$ ,then for $x < α$ (or) $x > β$ , $a x^{2} + b x + c$ and $a$ have ,
(A) Opposite sign
(B) Positive sign
(C) same sign
(D) none of these
Arational numbers
Breal and negative
Cnegative real parts
Dnone of these
If $α$ and $β$ are the roots of the equation $a x^{2} + b x + c = 0$ , then $\frac{α}{α β + b} + \frac{β}{a α + b}$ is equal to
A $\frac{2}{a}$
B $\frac{2}{b}$
C $\frac{2}{c}$
D $- \frac{2}{a}$