If dydx+Py=Q where P and Q are functions of x alone then integrating factor I.F. =e∫pdx
where elogx=x,e2logx=elogx2=x2,e−logx=x−1
Match the following:
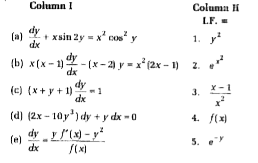
Text Solution
The correct Answer is:(a)→2,(b)→3,(c)→(5),(d)→1,(e)→4
|
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBOOK - ML KHANNACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Problem Set (2) (TRUE AND FALSE)
9 Videos
- DIFFERENTIAL EQUATIONSBOOK - ML KHANNACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Problem Set (2) (FILL IN THE BLANKS)
10 Videos
- DIFFERENTIAL EQUATIONSBOOK - ML KHANNACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Problem Set (1) (FILL IN THE BLANKS)
9 Videos
- DETERMINANTS BOOK - ML KHANNACHAPTER - DETERMINANTS EXERCISE - Self Assessment Test
19 Videos
- DIFFERENTIATIONBOOK - ML KHANNACHAPTER - DIFFERENTIATIONEXERCISE - MESCELLANEOUS EXERCISE
3 Videos
Similar Questions
Knowledge Check
∫e2elogxdx=
A1Be2Ce2−1D1+e2
∫(exloga+ealogx)dx
View SolutionIntegrate the functionse5logx−e4logxe2logx−e2logx
View Solution∫ex2+lnxdx
View Solution(2) ∫exlogedx
View Solution∫ealogx+exloga dx is equal to
View Solution(i) ∫ex[elogx+2]dx
View SolutionThe integrating factor of the differential equation dydx(x(log)ex)+y=2(log)ex is given by
View Solution
