For two data sets each of size 5, then variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4 respectively the variance of the combined data set is
52
112
6
132
The correct Answer is:B
To find the variance of the combined data set from two separate data sets, we can follow these steps:
Step 1: Identify the given data
We have two data sets, each of size 5. The variances and means are given as follows:
- Variance of the first data set (Var1) = 4
- Variance of the second data set (Var2) = 5
- Mean of the first data set (Mean1) = 2
- Mean of the second data set (Mean2) = 4
Step 2: Calculate the total number of observations
Since each data set has 5 observations, the total number of observations (N) in the combined data set is:
N=5+5=10
Step 3: Calculate the sum of the observations
Using the means, we can find the sum of the observations for both data sets:
- Sum of the first data set (Sum1) = Mean1 × Size = 2 × 5 = 10
- Sum of the second data set (Sum2) = Mean2 × Size = 4 × 5 = 20
Step 4: Calculate the combined mean
The combined mean (Mean_combined) can be calculated as:
Mean_combined=Sum1+Sum2N=10+2010=3010=3
Step 5: Calculate the sum of squares for both data sets
The formula for variance is:
Variance=Sum of squaresN−Mean2
We can rearrange this to find the sum of squares:
Sum of squares=Variance×N+Mean2×N
For the first data set:
Sum of squares1=Var1×5+Mean12×5=4×5+22×5=20+20=40
For the second data set:
Sum of squares2=Var2×5+Mean22×5=5×5+42×5=25+80=105
Step 6: Calculate the total sum of squares for the combined data set
The total sum of squares for the combined data set is:
Total Sum of squares=Sum of squares1+Sum of squares2=40+105=145
Step 7: Calculate the variance of the combined data set
Now, we can calculate the variance of the combined data set using the total sum of squares:
Variance_combined=Total Sum of squaresN−Mean_combined2
Variance_combined=14510−32
Variance_combined=14.5−9=5.5
Step 8: Express the variance in fractional form
The variance can be expressed as:
Variance_combined=5.5=112
Final Answer
The variance of the combined data set is 112.
---
We have two data sets, each of size 5. The variances and means are given as follows:
- Variance of the first data set (Var1) = 4
- Variance of the second data set (Var2) = 5
- Mean of the first data set (Mean1) = 2
- Mean of the second data set (Mean2) = 4
Since each data set has 5 observations, the total number of observations (N) in the combined data set is:
N=5+5=10
Using the means, we can find the sum of the observations for both data sets:
- Sum of the first data set (Sum1) = Mean1 × Size = 2 × 5 = 10
- Sum of the second data set (Sum2) = Mean2 × Size = 4 × 5 = 20
The combined mean (Mean_combined) can be calculated as:
Mean_combined=Sum1+Sum2N=10+2010=3010=3
The formula for variance is:
Variance=Sum of squaresN−Mean2
We can rearrange this to find the sum of squares:
Sum of squares=Variance×N+Mean2×N
Sum of squares1=Var1×5+Mean12×5=4×5+22×5=20+20=40
Sum of squares2=Var2×5+Mean22×5=5×5+42×5=25+80=105
The total sum of squares for the combined data set is:
Total Sum of squares=Sum of squares1+Sum of squares2=40+105=145
Now, we can calculate the variance of the combined data set using the total sum of squares:
Variance_combined=Total Sum of squaresN−Mean_combined2
Variance_combined=14510−32
Variance_combined=14.5−9=5.5
The variance can be expressed as:
Variance_combined=5.5=112
The variance of the combined data set is 112.
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - ASSERTION / REASON1videos
MEASURES OF CENTRAL TENDENCY
- BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - Problem Set (1) (Measures of Disperation)23videos
MEASURES OF CENTRAL TENDENCY
- BOOK - ML KHANNACHAPTER - MAXIMA AND MINIMA EXERCISE - MISCELANEOUS EXERCISE (COMPREHENSION)3videos
MAXIMA AND MINIMA
- BOOK - ML KHANNACHAPTER - NUMERICAL METHODSEXERCISE - SELF ASSESSMENT TEST10videos
NUMERICAL METHODS
Similar Questions
For two data sets, each of size 5, the variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4, respectively. The variance of the combined data set is
View SolutionFor two data sets, each of size 5, the variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4, respectively. The variance of the combined data set is (1) 112 (2) 2 (3) 132 (4) 52
View Solution
Knowledge Check
- Question 1 - Select One
Two data sets each of size 10 has the variance as 4 and k and the corresponding means as 2 and 4 respectively. If the variance of the combined data set is 5.5, then the value of k is equal to
A5B6C4D3 - Question 2 - Select One
If 2 data sets having 10 and 20 observation have coefficients of variation 50 and 60 respectively and arithmetic means 30 and 25 respectively, then the combined variance of those 30 observation is
A20753B20759C10009D10753
For two data sets, each with size 5, the variances are given to be 3 and 4 and the corresponding means are given 2 and 4, respectively. The variance of the combined data set is
View SolutionVariance of the data 2,4,6,8,10 is
View SolutionVariance of the data 2,4,6,8,10 is
View SolutionFind the mean and variance for each of the data :
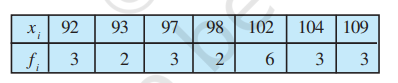 View Solution
View SolutionFind the mean and variance for each of the data :
 View Solution
View SolutionThe mean of two samples of sizes 200 and 300 were found to be 25,10 respectively. Their standard deviation were 3 and 4 respectively. The variance of combined sample of size 500 is
View Solution

