Find the solution set of the following system of linear inequations.
5x+12y≥20
3x+8y≤40
x≥0
y≥0
To find the solution set of the given system of linear inequalities, we will follow these steps:
Step 1: Write the inequalities
The inequalities we need to solve are:
1. 5x+12y≥20
2. 3x+8y≤40
3. x≥0
4. y≥0
Step 2: Convert inequalities to equations
To graph the inequalities, we first convert them to equations:
1. 5x+12y=20
2. 3x+8y=40
Step 3: Find intercepts for the first equation
For the equation 5x+12y=20:
- To find the x-intercept, set y=0:
5x=20⟹x=4(Point: (4, 0))
- To find the y-intercept, set x=0:
12y=20⟹y=2012=53(Point: (0, 5/3))
Step 4: Find intercepts for the second equation
For the equation 3x+8y=40:
- To find the x-intercept, set y=0:
3x=40⟹x=403(Point: (40/3, 0))
- To find the y-intercept, set x=0:
8y=40⟹y=5(Point: (0, 5))
Step 5: Graph the lines
Now we will graph the lines:
- The line 5x+12y=20 passes through points (4, 0) and (0, 5/3).
- The line 3x+8y=40 passes through points (40/3, 0) and (0, 5).
Step 6: Determine the feasible region
We need to determine the region that satisfies all inequalities:
1. For 5x+12y≥20, shade the area above the line.
2. For 3x+8y≤40, shade the area below the line.
3. The conditions x≥0 and y≥0 restrict us to the first quadrant.
Step 7: Find the intersection points
To find the vertices of the feasible region, we need to find the intersection of the two lines:
1. Solve the equations:
5x+12y=20(1)
3x+8y=40(2)
Multiply (1) by 3 and (2) by 5 to eliminate x:
15x+36y=60(3)
15x+40y=200(4)
Subtract (3) from (4):
4y=140⟹y=35
Substitute y=35 back into (1) or (2) to find x:
5x+12(35)=20⟹5x+420=20⟹5x=−400⟹x=−80(not feasible)
Step 8: Identify the vertices of the feasible region
The vertices of the feasible region are:
- (0, 0)
- (4, 0)
- (0, 5/3)
- (40/3, 0)
- (0, 5)
Step 9: Conclusion
The solution set of the system of inequalities is the area in the first quadrant bounded by the lines 5x+12y=20 and 3x+8y=40, along with the axes.
The inequalities we need to solve are:
1. 5x+12y≥20
2. 3x+8y≤40
3. x≥0
4. y≥0
To graph the inequalities, we first convert them to equations:
1. 5x+12y=20
2. 3x+8y=40
For the equation 5x+12y=20:
- To find the x-intercept, set y=0:
5x=20⟹x=4(Point: (4, 0))
- To find the y-intercept, set x=0:
12y=20⟹y=2012=53(Point: (0, 5/3))
For the equation 3x+8y=40:
- To find the x-intercept, set y=0:
3x=40⟹x=403(Point: (40/3, 0))
- To find the y-intercept, set x=0:
8y=40⟹y=5(Point: (0, 5))
Now we will graph the lines:
- The line 5x+12y=20 passes through points (4, 0) and (0, 5/3).
- The line 3x+8y=40 passes through points (40/3, 0) and (0, 5).
We need to determine the region that satisfies all inequalities:
1. For 5x+12y≥20, shade the area above the line.
2. For 3x+8y≤40, shade the area below the line.
3. The conditions x≥0 and y≥0 restrict us to the first quadrant.
To find the vertices of the feasible region, we need to find the intersection of the two lines:
1. Solve the equations:
5x+12y=20(1)
3x+8y=40(2)
Multiply (1) by 3 and (2) by 5 to eliminate x:
15x+36y=60(3)
15x+40y=200(4)
Subtract (3) from (4):
4y=140⟹y=35
Substitute y=35 back into (1) or (2) to find x:
5x+12(35)=20⟹5x+420=20⟹5x=−400⟹x=−80(not feasible)
The vertices of the feasible region are:
- (0, 0)
- (4, 0)
- (0, 5/3)
- (40/3, 0)
- (0, 5)
The solution set of the system of inequalities is the area in the first quadrant bounded by the lines 5x+12y=20 and 3x+8y=40, along with the axes.
Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Practice Exercises
26 Videos
- LINEAR PROGRAMMING BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Fill in the blanks
9 Videos
- LIMITS, CONTINUITY AND DIFFERENTIABILITY BOOK - ML KHANNACHAPTER - LIMITS, CONTINUITY AND DIFFERENTIABILITY EXERCISE - MISCELLANEOUS EXERCISE (ASSERTION/ REASONS)
3 Videos
- LOGARITHMS AND SURDSBOOK - ML KHANNACHAPTER - LOGARITHMS AND SURDSEXERCISE - Miscellaneous exercise
3 Videos
Similar Questions
Knowledge Check
The solution set of the linear inequalities 2x+2y≥10 and x+2y≥10
A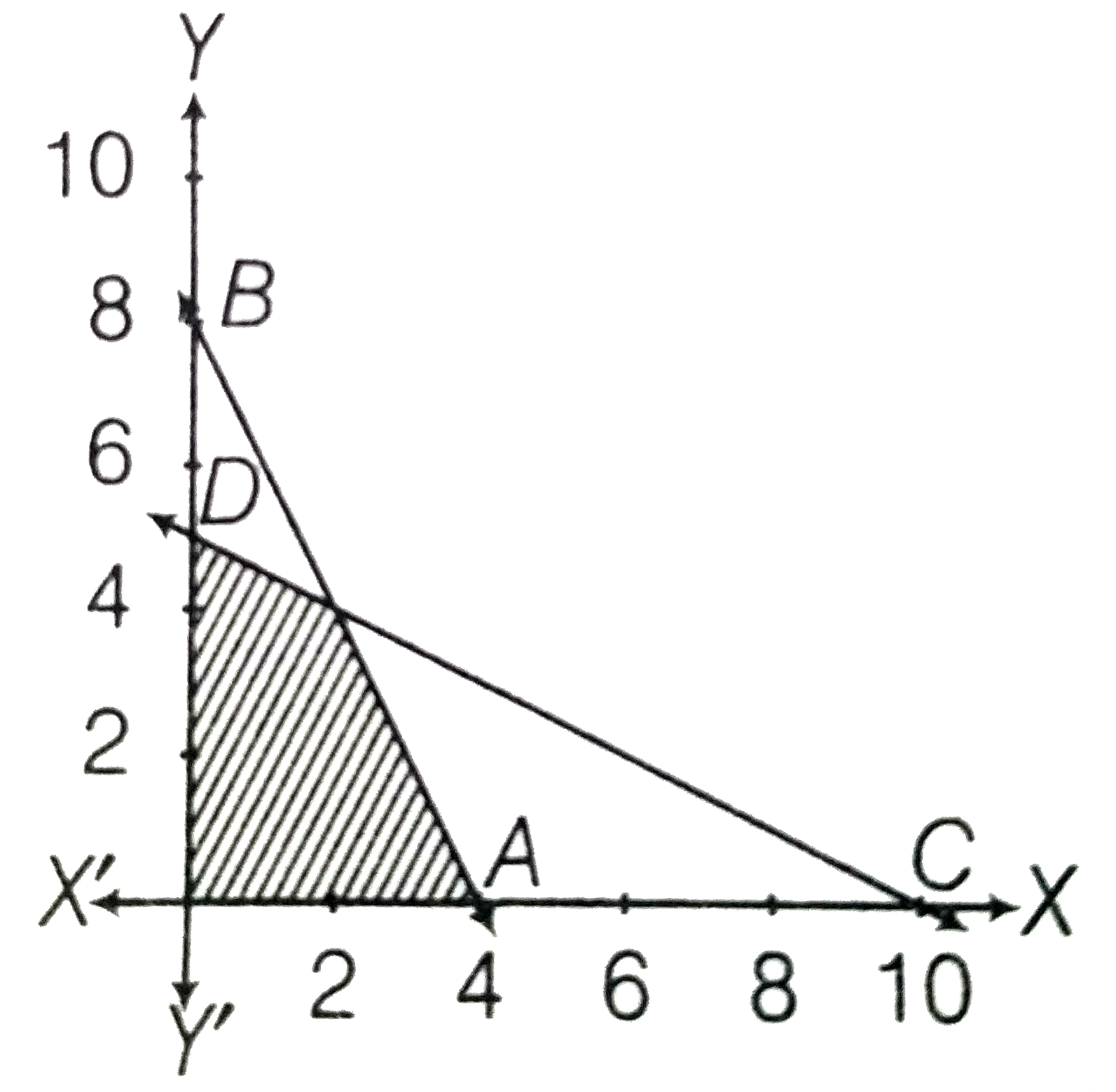 B
B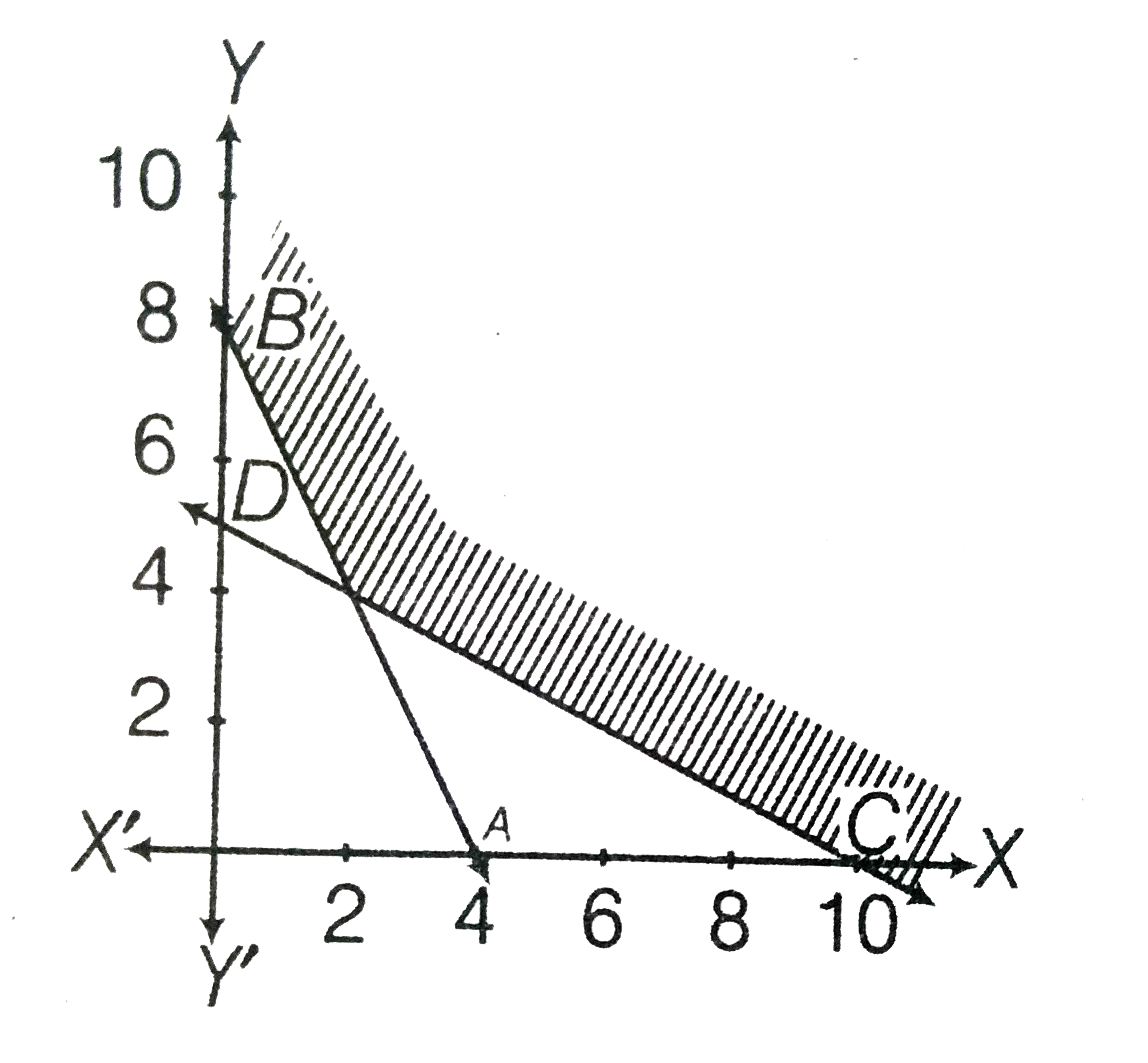 C
C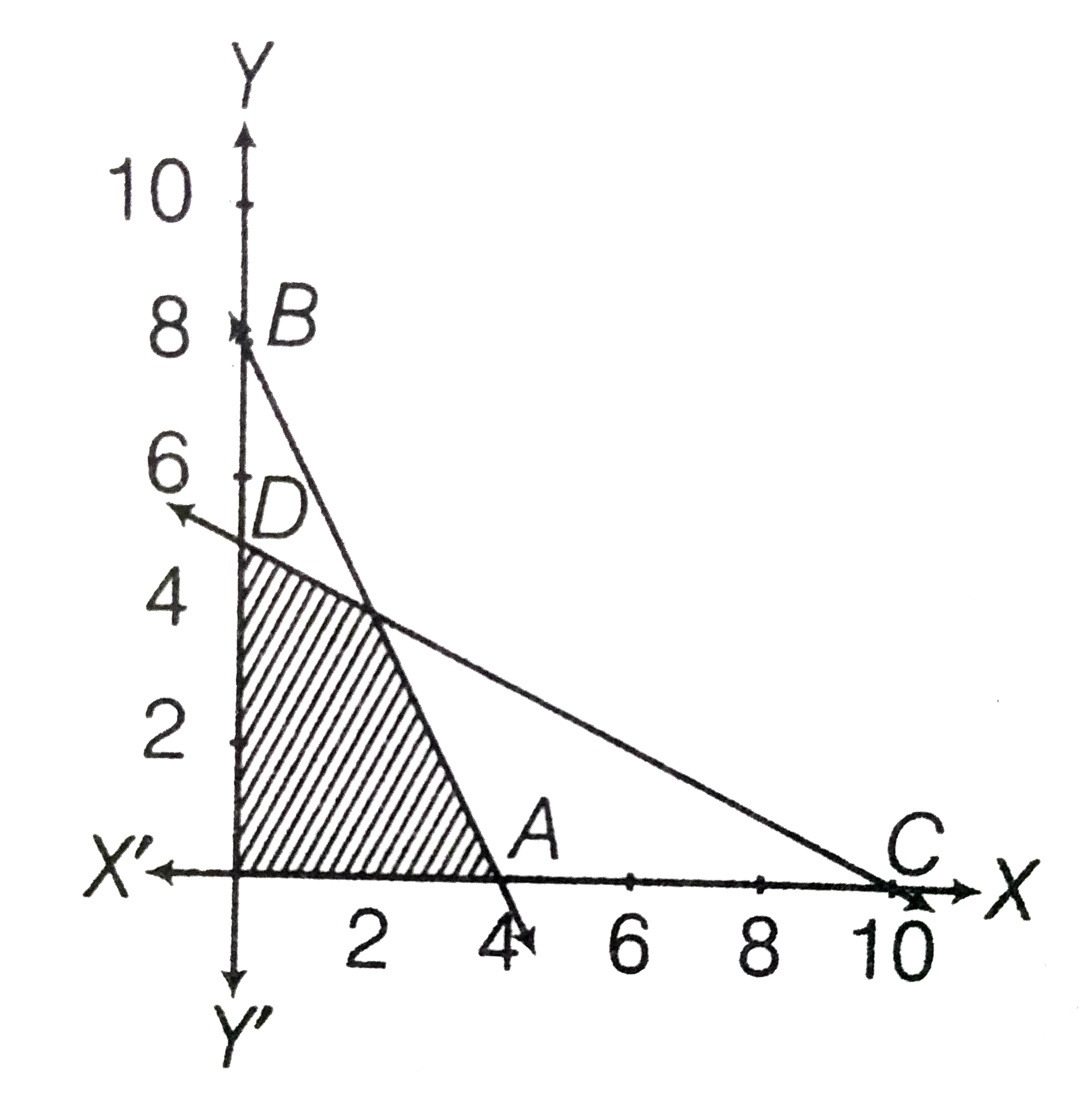 DNone of these
DNone of these
Solve the following system of inequtions graphically.
x+3y≤12,33x+y≤12,x≥0,y≥0
View SolutionSolve the following system of inequations graphically
x+y≤10,x+3y≤15,x≥0,y≥0
View SolutionShow that the following system of linear inequalities has no solution x+2y≤3,3x+4y≥12,x≥0,y≥1.
View SolutionFind graphically the solution sets of each of the following systems of inequalities :
x+y≤6
2x+5y≥−8
3x+8y≤9
10x+12y≤7
8x+7y≤14
x,y≥10
View Solutionx+2y≤40,2x+y≤40,x≥0,y≥0
View SolutionSolve the following system of inequalities graphically:
x+y≤200,x≤20,y≥4x,x≥0,y≥0.
View Solutionsolve the following system of inequation by graphical method:
2x+3y≤6,3x+2y≤6,x≥0,y≥0
View Solution