A point is moving with uniform acceleration, in the eleventh and fifteenth seconds from the commencement it moves through 720 and 960 cm respectively. Its initial velocity, and the acceleration with which it moves are
60, 40
70, 30
90, 60
None
The correct Answer is:C
To solve the problem, we need to find the initial velocity (U) and the acceleration (A) of a point moving with uniform acceleration. We know the distances covered in the 11th and 15th seconds of its motion.
Step 1: Understand the formula for distance covered in nth second
The distance covered in the nth second (S_n) can be expressed as:
Sn=U+A2(2n−1)
where:
- Sn is the distance covered in the nth second,
- U is the initial velocity,
- A is the acceleration,
- n is the second in which the distance is measured.
Step 2: Write equations for the 11th and 15th seconds
For the 11th second:
S11=U+A2(2⋅11−1)=720
This simplifies to:
S11=U+A2(22−1)=U+21A2=720
(Equation 1)
For the 15th second:
S15=U+A2(2⋅15−1)=960
This simplifies to:
S15=U+A2(30−1)=U+29A2=960
(Equation 2)
Step 3: Set up the equations
From the two equations we have:
1. U+21A2=720 (Equation 1)
2. U+29A2=960 (Equation 2)
Step 4: Subtract Equation 1 from Equation 2
Subtract Equation 1 from Equation 2 to eliminate U:
(U+29A2)−(U+21A2)=960−720
This simplifies to:
29A2−21A2=240
8A2=240
4A=240
A=60 cm/s2
Step 5: Substitute A back into one of the equations to find U
Now, substitute A=60 cm/s² back into Equation 1:
U+21⋅602=720
U+630=720
U=720−630
U=90 cm/s
Final Result
The initial velocity U is 90 cm/s and the acceleration A is 60 cm/s².
The distance covered in the nth second (S_n) can be expressed as:
Sn=U+A2(2n−1)
where:
- Sn is the distance covered in the nth second,
- U is the initial velocity,
- A is the acceleration,
- n is the second in which the distance is measured.
For the 11th second:
S11=U+A2(2⋅11−1)=720
This simplifies to:
S11=U+A2(22−1)=U+21A2=720
(Equation 1)
S15=U+A2(2⋅15−1)=960
This simplifies to:
S15=U+A2(30−1)=U+29A2=960
(Equation 2)
From the two equations we have:
1. U+21A2=720 (Equation 1)
2. U+29A2=960 (Equation 2)
Subtract Equation 1 from Equation 2 to eliminate U:
(U+29A2)−(U+21A2)=960−720
This simplifies to:
29A2−21A2=240
8A2=240
4A=240
A=60 cm/s2
Now, substitute A=60 cm/s² back into Equation 1:
U+21⋅602=720
U+630=720
U=720−630
U=90 cm/s
The initial velocity U is 90 cm/s and the acceleration A is 60 cm/s².
Similar Questions
A body moving with uniform acceleration a stratght line describes 25m in the fifth second and 33min the seventh second. Find its initial velocity an dacceleration.
View SolutionA body moving with uniform acceleration, travels 24 m in the 6th second and 44 m in the 11th second. At the nth second, find
(i) the acceleration and
(ii) the initial velocity of the bodyView Solution
Knowledge Check
- Question 1 - Select One
A body is moving with uniform acceleration. Its 'velocity
Awill be increasing,Bwill be decreasing,Cwill be uniform,Dwill increase first and decrease afterward. - Question 2 - Select One
A body starting from rest and moving with uniform acceleration will have
Av∝tBv∝sCv∝tDv∝√t - Question 3 - Select One
A body moves with uniform acceleration, which of the following graph is correct?
A B
B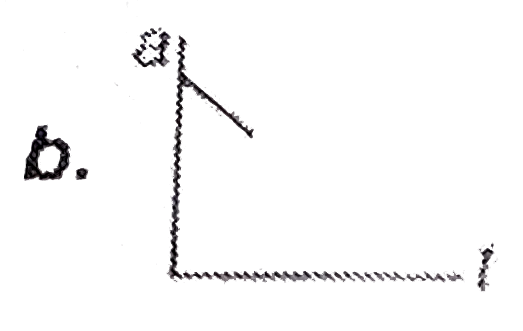 C
C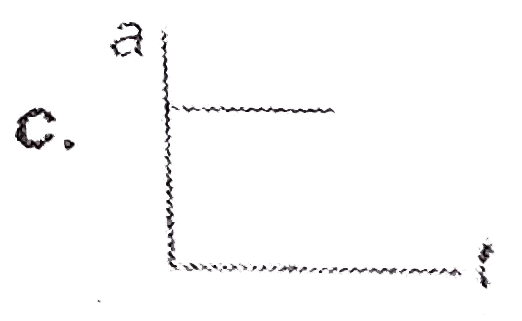 D
D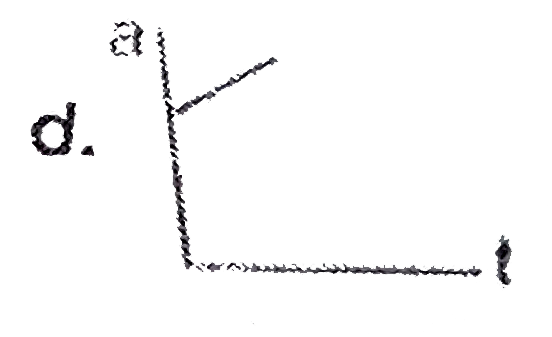
For body moving with uniform acceleration a, initial and final velocities in a time interval t are u and v respectively. Then its average velocity in the time interval t is
View SolutionA body is moving in a straight line with uniform acceleration. It covers distances of 10 m and 12 m in third and fourth second respectively, then the initial velocity in m/sec is
View SolutionA point moving with uniform acceleration, describes 25 cm in the half second which elapses after the first second of its motion, and 198 cm. in the eleventh second of its motion. Then the acceleration and its initial velocity in cm/sec are
View SolutionA body is moving with a uniform acceleration coverss 40m in the first 4 s and 120m in next 4s. Its initial velocity and acceleration are
View SolutionA particle moving with uniform acceleration has velocity of 6ms−1 at a distance 5 m from the initial position. After moving another 7 m the velocity becomes 8ms−1 The initial velocity and acceleration of the particle are
View Solution

