A projectile is fired horizontally from a tower which is 25 ft high from the level of the ground and reaches the ground at a horizontal distance of 1000 ft. The initial velocity is
200ft/sec
400ft/sec
600ft/sec
800ft/sec
The correct Answer is:D
To solve the problem of a projectile fired horizontally from a tower, we can break it down into a few steps:
Step 1: Understand the Problem
We have a projectile fired horizontally from a height of 25 feet, and it lands 1000 feet away from the base of the tower. We need to find the initial horizontal velocity of the projectile.
Step 2: Determine the Time of Flight
The time it takes for the projectile to fall can be calculated using the formula for vertical motion under gravity:
h=12gt2
Where:
- h=25 feet (height of the tower)
- g=32 feet/s² (acceleration due to gravity)
- t = time in seconds
Substituting the values into the equation:
25=12×32×t2
25=16t2
t2=2516
t=√2516=54 seconds
Step 3: Calculate the Initial Horizontal Velocity
The horizontal distance traveled by the projectile can be calculated using the formula:
d=u⋅t
Where:
- d=1000 feet (horizontal distance)
- u = initial horizontal velocity (what we need to find)
- t=54 seconds (time of flight)
Rearranging the formula to find u:
u=dt
Substituting the known values:
u=100054=1000×45=800 feet/second
Conclusion
The initial velocity of the projectile is 800 feet/second.
---
We have a projectile fired horizontally from a height of 25 feet, and it lands 1000 feet away from the base of the tower. We need to find the initial horizontal velocity of the projectile.
The time it takes for the projectile to fall can be calculated using the formula for vertical motion under gravity:
h=12gt2
Where:
- h=25 feet (height of the tower)
- g=32 feet/s² (acceleration due to gravity)
- t = time in seconds
25=12×32×t2
25=16t2
t2=2516
t=√2516=54 seconds
The horizontal distance traveled by the projectile can be calculated using the formula:
d=u⋅t
Where:
- d=1000 feet (horizontal distance)
- u = initial horizontal velocity (what we need to find)
- t=54 seconds (time of flight)
u=dt
Substituting the known values:
u=100054=1000×45=800 feet/second
The initial velocity of the projectile is 800 feet/second.
Similar Questions
A body is thrown horizontally from the top of a tower of height 5m. It touches the ground at a distance of 10m from the foot of the tower. Find the initial velocity of the body.
View SolutionA body is thrown horizontally from the top of a tower of height 5m. It touches the ground at a distance of 10 m from the foot of the tower. The initial velcotiy (in m/s) of the body is (g=10ms−2)
View Solution
Knowledge Check
A body, rpojected horizontally with a speed u from the top of a tower of height h, reaches the ground at a horizontally distance R from the tower. Another body, projected horizontally from the top of a tower of height 4h, reaches the ground at horizontal distance 2R from the tower. The initial speed of the second body is
AuB2uC3uD4uA body is projected horizontally from a height of 20m. It reaches the ground at a horizontally distance of 40m. The speed of practicle when it hits the ground is
A10m/sB10√m/sC20m/sD20√2m/sA body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If a second body of mass 2m is projected horizontally from the top of a tower of height 2h, it reaches the ground at a distance 2x from the foot of the tower. The horizontal velocity of the second body is :
AvB2 vC√2vDv//2
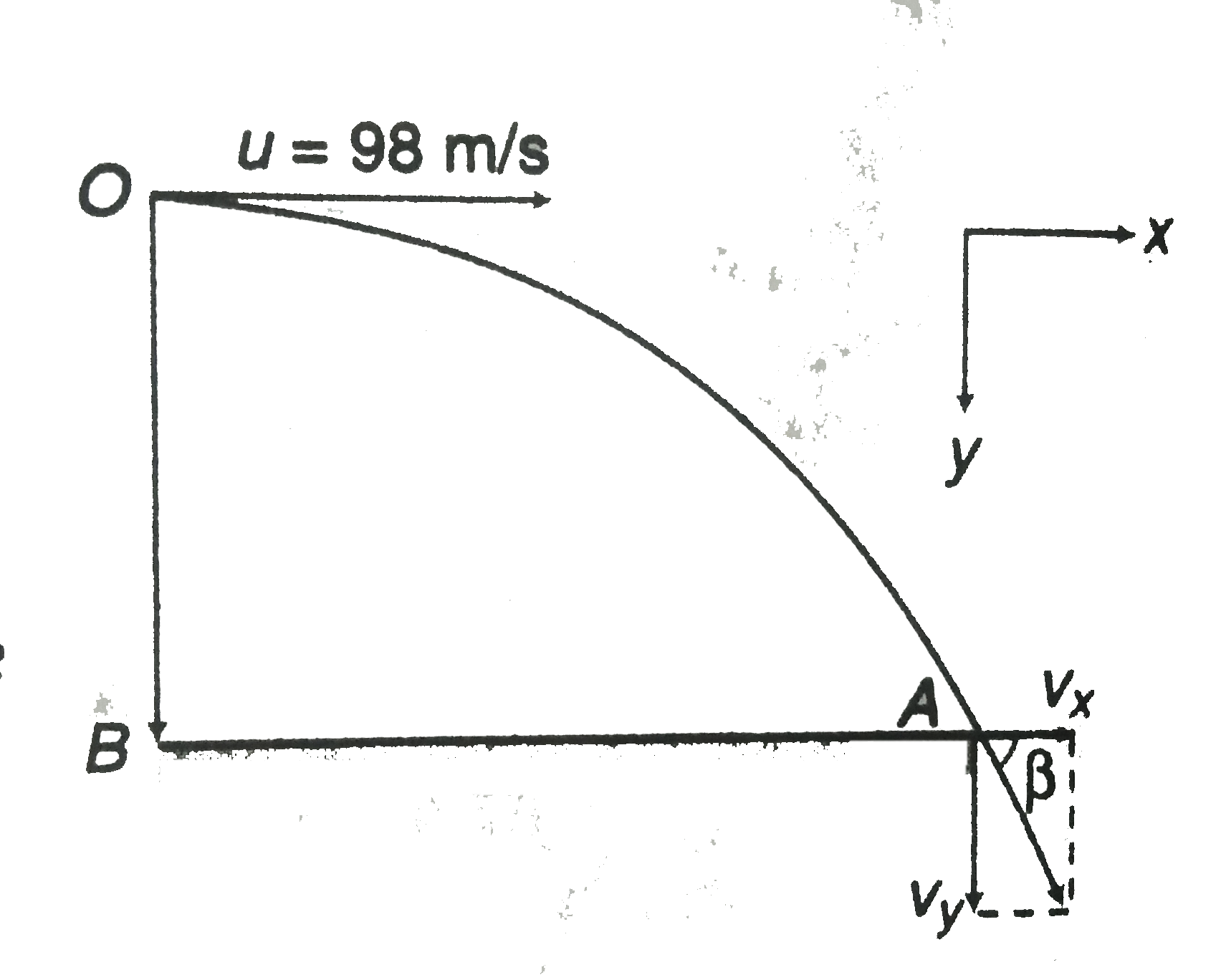
A projectile is fired horizontally with a velocity of 98ms−1 from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View SolutionFrom the top of a hill 480 m high , a projectile is fired horizontally with a speed of 96m/s . Calculate
(i) the time taken by projectile to reach the ground .
(ii) the distance of the target from the hill .
(iii) the velocity with which the projectile hits the ground . Take g=10ms−2
View SolutionA ball is thrown horizontally from a point 100m above the ground with a speed of 20m/s. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground.
View SolutionA body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If a second body of mass 2m is projected horizontally from the top of a tower of height 2h, it reaches the ground at a distance 2x from the foot of the tower. The horizontal velocity of the second body is :
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. (g=9.8m/s2)
 .
.
View Solution
