A particle is projected with a velocity of 39.2m/sec at an angle of 30∘ to the horizontal. It will move at right angles to the direction of projection after the time
8 sec
5 sec
6 sec
10 sec
The correct Answer is:A
To solve the problem of a particle projected with a velocity of 39.2ms at an angle of 30° to the horizontal, we need to determine the time at which the particle's velocity becomes perpendicular to its initial velocity. Here’s a step-by-step solution:
Step 1: Break down the initial velocity into components
The initial velocity u can be broken down into horizontal and vertical components using trigonometric functions:
- ux=ucos(θ)
- uy=usin(θ)
Given:
- u=39.2m/s
- θ=30°
Calculating the components:
- ux=39.2cos(30°)=39.2×√32=19.6√3m/s
- uy=39.2sin(30°)=39.2×12=19.6m/s
Step 2: Determine the velocity components at time t
The horizontal component of velocity remains constant:
- vx=ux=19.6√3m/s
The vertical component of velocity changes due to gravity:
- vy=uy−gt
Where g=9.8m/s2.
Thus,
- vy=19.6−9.8t
Step 3: Set up the condition for perpendicularity
For the two velocity vectors to be perpendicular, their dot product must equal zero:
uxvx+uyvy=0
Substituting the known values:
(19.6√3)(19.6√3)+(19.6)(19.6−9.8t)=0
Step 4: Simplify the equation
Expanding the equation gives:
19.62⋅3+19.62−19.6⋅9.8t=0
Combining like terms:
19.62(3+1)−19.6⋅9.8t=0
19.62⋅4−19.6⋅9.8t=0
Step 5: Solve for t
Factoring out 19.6:
19.6(19.6⋅4−9.8t)=0
Since 19.6≠0, we can set the remaining factor to zero:
19.6⋅4−9.8t=0
9.8t=19.6⋅4
t=19.6⋅49.8
t=78.49.8=8s
Final Answer
The time at which the particle moves at right angles to the direction of projection is 8 seconds.
The initial velocity u can be broken down into horizontal and vertical components using trigonometric functions:
- ux=ucos(θ)
- uy=usin(θ)
- u=39.2m/s
- θ=30°
- ux=39.2cos(30°)=39.2×√32=19.6√3m/s
- uy=39.2sin(30°)=39.2×12=19.6m/s
The horizontal component of velocity remains constant:
- vx=ux=19.6√3m/s
- vy=uy−gt
Where g=9.8m/s2.
- vy=19.6−9.8t
For the two velocity vectors to be perpendicular, their dot product must equal zero:
uxvx+uyvy=0
(19.6√3)(19.6√3)+(19.6)(19.6−9.8t)=0
Expanding the equation gives:
19.62⋅3+19.62−19.6⋅9.8t=0
19.62(3+1)−19.6⋅9.8t=0
19.62⋅4−19.6⋅9.8t=0
Factoring out 19.6:
19.6(19.6⋅4−9.8t)=0
19.6⋅4−9.8t=0
9.8t=19.6⋅4
t=19.6⋅49.8
t=78.49.8=8s
The time at which the particle moves at right angles to the direction of projection is 8 seconds.
Similar Questions
Knowledge Check
A particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1mA particle is projected with a velocity of 30 m/s at an angle θ with the horizontal . Where θ=tan−1(34) . After 1 second, direction of motion of the particle makes an angle α with the horizontal then α is given by
Atanα=13Btanα=12Ctanα=2Dtanα=1
If a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionA particle is projected with a velocity of 20√3ms−1 at an angle of 60∘ to the horizontal. At the moment, the direction of motion of the projectile is perpendicular to the direction of initial velocity of projection, its velocity is
View SolutionA particle is projected with a velocity of 20√3ms−1 at an angle of 60∘ to the horizontal.At the moment,the direction of motion of the projectile is perpendicular to the direction of initial velocity of projection, its velocity is?
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected with a velocity of 39.2 m/sec at an elevation of 30°. Find (i) the time of flight. (ii) the greatest height.
View SolutionA particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
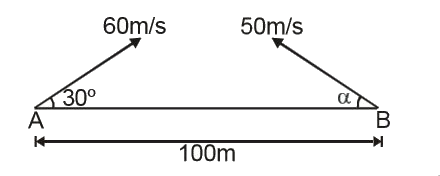
View Solution
