An aeroplane A is flying at a level height towards north with a velocity of 800 km./hr as observed from the ground. Its pilot observes that another aeroplane B at the same height appears 10 him to be flying towards west with a velocity of 600 km/hr., The direction and magnitude of the velocity of the aeroplane B as observed from the ground are
500,tan−134
1100,tan−143
100,tan−143
none
The correct Answer is:C
To find the direction and magnitude of the velocity of aeroplane B as observed from the ground, we can use vector addition.
1. Identify the velocities:
- The velocity of aeroplane A (V_A) is 800 km/hr towards the north.
- The velocity of aeroplane B (V_B) appears to the pilot of A to be 600 km/hr towards the west.
2. Set up a coordinate system:
- Let north be the positive y-direction and east be the positive x-direction.
- Therefore, the velocity of A can be represented as:
VA=0^i+800^j km/hr
- The velocity of B as observed from A can be represented as:
VB/A=−600^i+0^j km/hr
3. Use the relative velocity formula:
- The velocity of B as observed from the ground (V_B) can be found using the formula:
VB=VA+VB/A
- Substituting the values:
VB=(0^i+800^j)+(−600^i+0^j)
VB=−600^i+800^j km/hr
4. Calculate the magnitude of V_B:
- The magnitude of the velocity vector can be calculated using the Pythagorean theorem:
|VB|=√(−600)2+(800)2
|VB|=√360000+640000=√1000000=1000 km/hr
5. Determine the direction of V_B:
- The direction can be found using the tangent function:
tan(θ)=oppositeadjacent=800600
θ=tan−1(800600)=tan−1(43)
- Calculating this gives:
θ≈53.13∘
- Since V_B has a negative x-component and a positive y-component, it is in the second quadrant. Thus, the direction of V_B is:
180∘−53.13∘=126.87∘ from the positive x-axis (east)
Final Answer:
- The magnitude of the velocity of aeroplane B as observed from the ground is 1000 km/hr.
- The direction is approximately 126.87° from the positive x-axis (east), or equivalently, 53.13° north of west.
- The velocity of aeroplane A (V_A) is 800 km/hr towards the north.
- The velocity of aeroplane B (V_B) appears to the pilot of A to be 600 km/hr towards the west.
- Let north be the positive y-direction and east be the positive x-direction.
- Therefore, the velocity of A can be represented as:
VA=0^i+800^j km/hr
- The velocity of B as observed from A can be represented as:
VB/A=−600^i+0^j km/hr
- The velocity of B as observed from the ground (V_B) can be found using the formula:
VB=VA+VB/A
- Substituting the values:
VB=(0^i+800^j)+(−600^i+0^j)
VB=−600^i+800^j km/hr
- The magnitude of the velocity vector can be calculated using the Pythagorean theorem:
|VB|=√(−600)2+(800)2
|VB|=√360000+640000=√1000000=1000 km/hr
- The direction can be found using the tangent function:
tan(θ)=oppositeadjacent=800600
θ=tan−1(800600)=tan−1(43)
- Calculating this gives:
θ≈53.13∘
- Since V_B has a negative x-component and a positive y-component, it is in the second quadrant. Thus, the direction of V_B is:
180∘−53.13∘=126.87∘ from the positive x-axis (east)
- The magnitude of the velocity of aeroplane B as observed from the ground is 1000 km/hr.
- The direction is approximately 126.87° from the positive x-axis (east), or equivalently, 53.13° north of west.
Similar Questions
A man going east in a car with a velocity of 20 km/hr, a train appears to him to move towards north with a velocity of 20√3 km/hr. What is the actual velocity and direction of motion of train?
View SolutionAn aeroplane is flying horizontally at a height of 23km with a velocity of 15 km/h. Find the rate at which it is receding from a fixed point on the ground which it passed over 2 min ago.
View Solution
Knowledge Check
- Question 1 - Select One
A man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
A7 km/hrB5 km/hrC4/3 km/hrD3/4 km/hr - Question 2 - Select One
A bird is flying towards south with a velocity 40km/hr and a train is moving with a velocity 40km/hr towards east. What is the velocity of the bird w.r.t. an obserber in train:-
A40√2 km/hr. North-EastB40√2 km/hr. South-EastC40√2 km/hr. South -WestD40√2 km/hr. North-West - Question 3 - Select One
What was the name of the aeroplane that the pilot was flying?
AAirbusBBoeingCDakotaDMinesotta
To a person, going eastward in a car with a velociyt of 25km/hr, a train appears to move towards north with a velocity of 25√3km/hr. The actual velocity of the train will be
View SolutionA persons walks at the rate of 3km/hr. Rain appears to him in vertical direction at the rate of 3√3km/hr. Find magnitude and direction of true velocity of rain.
View SolutionAn aeroplne A is flying horizontally due east at a speed of 400km/hr.Passengers in A, observe another aeroplane B moving perpendicular to direction of motion of A.Aeroplane B is actually moving in a direction 30∘ north of east in the same horizontal plane as shown in the figure.Determine the velocity of B
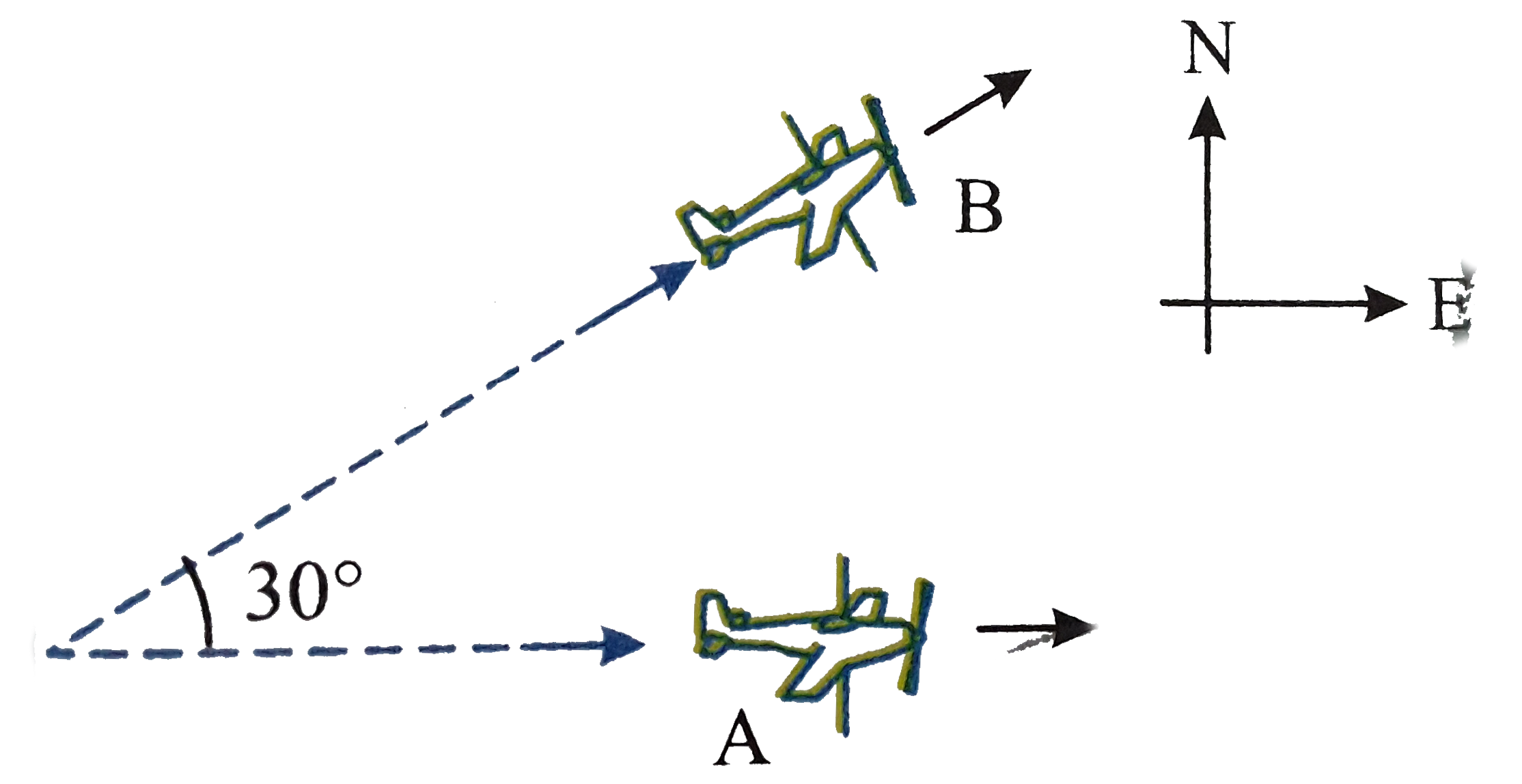 View Solution
View SolutionAn aeroplane is flying at a height of 1960 m in horizontal direction with a velocity of 360 km/hr. When it is vertically above the point. A on the ground, it drops a bomb. The bomb strikes a point B on the ground, then the time taken by the bomb to reach the ground is-
View SolutionAn aeroplane is flying with the velocity of V1=800kmph relative to the air towards south.A wind with velocity of V2=15ms−1 is blowing from west to east.What is the velocity of the aeroplane with respect of the earth.
View Solution

