Forces proportional to AB, BC and 2CA act along the sides of triangle ABC in order, their resultants represented in magnitude and direction is
CA
AC
BC
CB
The correct Answer is:A
To solve the problem, we need to find the resultant of the forces acting along the sides of triangle ABC, which are proportional to the lengths of the sides AB, BC, and 2CA.
1. Identify the Forces:
- Let the length of side AB = c, BC = a, and CA = b.
- The forces acting along the sides are:
- F1 (along AB) = k * c (where k is a proportionality constant)
- F2 (along BC) = k * a
- F3 (along CA) = 2k * b
2. Determine the Directions of Forces:
- F1 acts along AB.
- F2 acts along BC.
- F3 acts along CA but in the opposite direction (since it is acting along CA).
3. Resolve the Forces into Components:
- We can resolve these forces into their horizontal (x) and vertical (y) components.
- Assuming angle A is at vertex A, angle B at vertex B, and angle C at vertex C, we can use trigonometric functions to resolve the forces:
- F1:
- F1x = F1 * cos(A)
- F1y = F1 * sin(A)
- F2:
- F2x = F2 * cos(B)
- F2y = F2 * sin(B)
- F3 (acting in the opposite direction):
- F3x = -F3 * cos(C)
- F3y = -F3 * sin(C)
4. Calculate the Resultant Components:
- Sum the x-components:
- Rx = F1x + F2x + F3x
- Sum the y-components:
- Ry = F1y + F2y + F3y
5. Calculate the Magnitude of the Resultant Force:
- The magnitude of the resultant force R can be found using Pythagoras' theorem:
- R = √(Rx² + Ry²)
6. Determine the Direction of the Resultant Force:
- The direction (angle θ) of the resultant can be calculated using:
- θ = tan⁻¹(Ry/Rx)
Final Result:
The resultant force R has a magnitude of √(Rx² + Ry²) and an angle θ with respect to the horizontal axis.
- Let the length of side AB = c, BC = a, and CA = b.
- The forces acting along the sides are:
- F1 (along AB) = k * c (where k is a proportionality constant)
- F2 (along BC) = k * a
- F3 (along CA) = 2k * b
- F1 acts along AB.
- F2 acts along BC.
- F3 acts along CA but in the opposite direction (since it is acting along CA).
- We can resolve these forces into their horizontal (x) and vertical (y) components.
- Assuming angle A is at vertex A, angle B at vertex B, and angle C at vertex C, we can use trigonometric functions to resolve the forces:
- F1:
- F1x = F1 * cos(A)
- F1y = F1 * sin(A)
- F2:
- F2x = F2 * cos(B)
- F2y = F2 * sin(B)
- F3 (acting in the opposite direction):
- F3x = -F3 * cos(C)
- F3y = -F3 * sin(C)
- Sum the x-components:
- Rx = F1x + F2x + F3x
- Sum the y-components:
- Ry = F1y + F2y + F3y
- The magnitude of the resultant force R can be found using Pythagoras' theorem:
- R = √(Rx² + Ry²)
- The direction (angle θ) of the resultant can be calculated using:
- θ = tan⁻¹(Ry/Rx)
The resultant force R has a magnitude of √(Rx² + Ry²) and an angle θ with respect to the horizontal axis.
Similar Questions
If AB,BC,CA are three sides of triangle ABC having length 10,7,8 respectively then the projection of sides AB on BC is
View SolutionThree forces P,2P and 3P act along the sides AB, BC and CA of a given equilateral triangle ABC, The magnitude and direction of their resultant and also the point in which its line of action meets the side BC are ........... , ........ and ..........
View Solution
Knowledge Check
Forces proportional to AB, BC & 2 CA act along the sides of triangle ABC in order, their resultant represented in magnitude and direction as:
ACABACCBCDCBForces proportional to AB,BC and 2CA act along the slides of a triangle ABC in magnitude and direction by
ACABACCBCDCBThree forces start acting simultaneously on a particle moving the velocity →V. The forces are represented in magnitude and direction by the three sides of a triangle ABC (as shown). The particle will now move with velocity
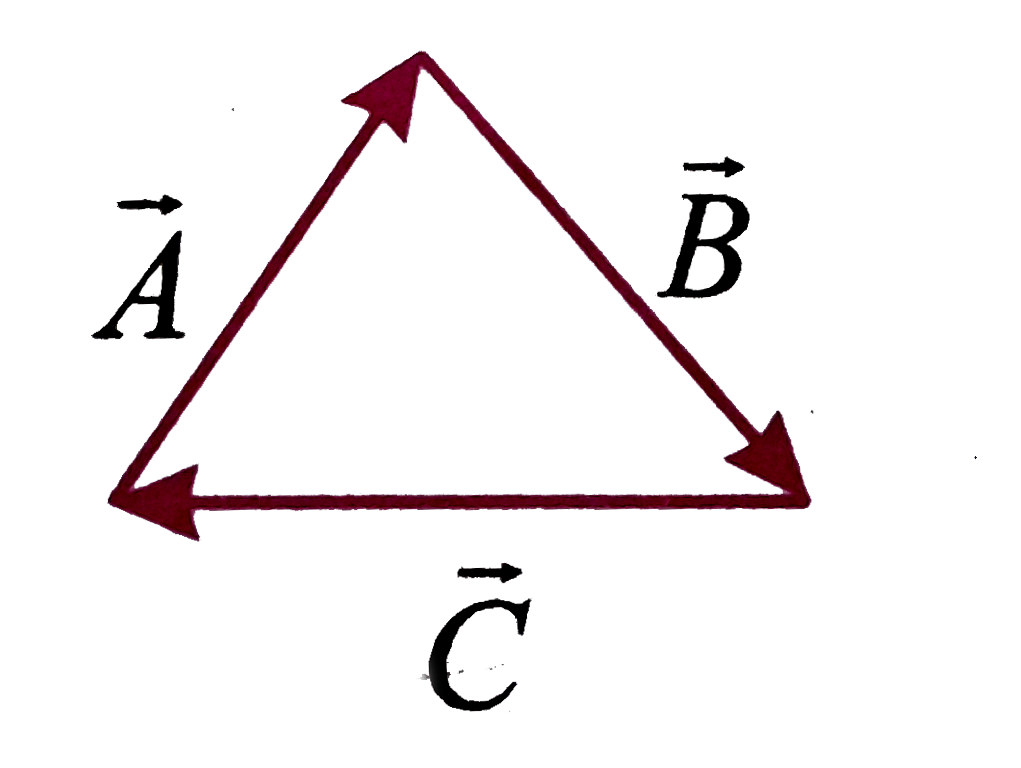 Aless than →VBgreater than →VC∣∣→V∣∣ in the direction of largest forceD→V remaining unchanged
Aless than →VBgreater than →VC∣∣→V∣∣ in the direction of largest forceD→V remaining unchanged
Three forces P, Q, R act along the sides BC, CA, AB of a triangle ABC taken in order :
Write the conditions so that the resultant passes. Through
the incentre, ………
View SolutionThree forces P, Q, R act along the sides BC, CA, AB of a triangle ABC taken in order :
Write the conditions so that the resultant passes. through
the circumcentre, ……….
View SolutionThree forces start acting simultaneously on a particle moving with velocity, ¯v. These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity
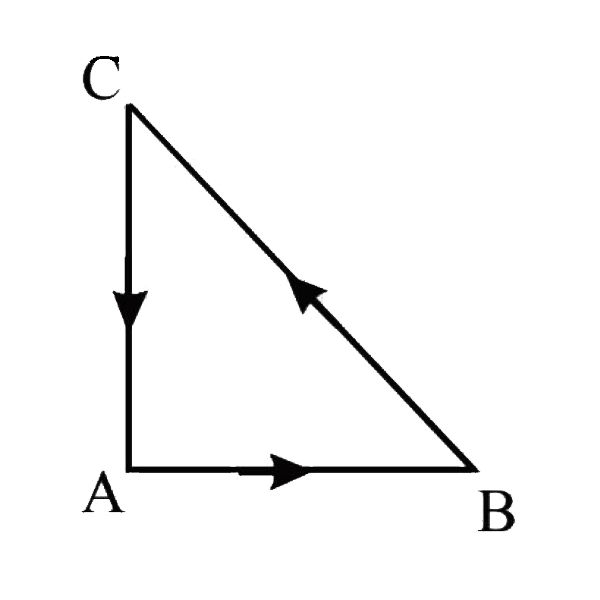
View SolutionThe resultant of two forces sec B and C along sides AB , AC of triangle ABC is a force acting along AD when D is
View SolutionThree forces start acting simultaneously on a particle moving with velocity v. These forces are represented in magnitude and direction by the three sides of a triangle ABC (as shown). The particle will now move with velocity.
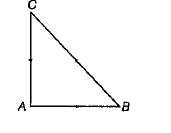
View Solution
