Derive the equation $x = x_{0} + u t + \frac{1}{2} a t^{2} or s = u t + \frac{1}{2} a t^{2} .$

Text Solution

Verified by Experts

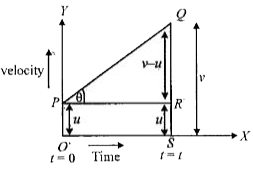
Let $x_{0}$ is position of particle at t = 0 and x is position at time t.
Distance travelled in time t = Area under OPQS region
= Area of rectangle OPRS + Area of triangle PQR
$= (P R + R S) + \frac{1}{2} (Q R + P R)$
From PR = t
RS = u
$Q R = v - u$
$x - x_{0} = u t + \frac{1}{2} (v - u 0 . t (∵ v - u = a t)$
$x - x_{0} = u t + \frac{1}{2} a t^{2} .$
$s =$ distance covered $= x - x_{0} u t + \frac{1}{2} a t^{2} .$

Updated on:21/07/2023

|

Class 11 PHYSICS RECTILINEAR MOTION

Similar Questions

Knowledge Check

In $S = u t + \frac{1}{2} a t^{2}$ , $S = 96, t = 8 and a = 2$ , find u.
A2
B8
C4
D1
In the equation of motion, S=ut+1/2 at^(2), s stands for
Adistance in t seconds
Bmaximum height reached
Cdistance in the $t^{t h}$ second
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile