Derive the relation s=ut+12at2 for uniformly accelerated motion along a straight line. Solution in Punjabi
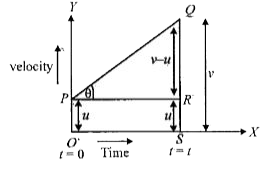
Let x0 is position of particle at t = 0 and x is position at time t.
Distance travelled in time t = Area under OPQS region
= Area of rectangle OPRS + Area of triangle PQR
=(PR+RS)+12(QR+PR)
From PR = t
RS = u
QR=v−u
x−x0=ut+12(v−ut)(∵v−u=at)
x−x0=ut+12at2.
s= distance covered =x−x0ut+12at2.
Similar Questions
Derive the following equations of motion for uniformly accelerated motion from velocity-time graph : s = ut + 1/2 at^(2)
04:35View SolutionFor uniform accelerated motion, draw by graphical method establish the following equations of motion: S= ut+frac(1)(2)at^2 .
08:12View SolutionUsing velocity time graph, derive the equations of motion for uniform acceleration moving along a straight line.
11:27View SolutionIn the equation of motion, S=ut+1/2 at^(2), s stands for
01:34View SolutionDerive following equations for a uniformly accelerated motion : (i) v = u + at (ii) S = ut+(1)/(2) at^(2) (iii) v^(2)= u^(2) +2aS Where the symbols have their usual meanings .
06:12View SolutionDerive the following relations for uniformly accelerated motion.
Velocity-time relation02:21View SolutionDerive the following relations for uniformly accelerated motion.
Displacement-time relation.03:12View SolutionDerive the relation s=ut+12at2 for uniformly accelerated motion along a straight line.
03:00View Solution

