Discuss the motion of charge particle in uniform mangetic field, wen it moves at an angle $θ$ with the direction of magnetic field. Prove that its path is helical. Calculate the pitch of helical path. What will be the nature of path if $(i) θ = 90^{\circ} and (i i) θ = 180^{\circ} .$

Text Solution

Verified by Experts

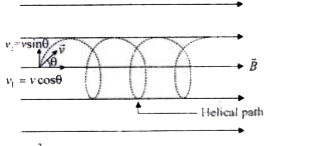
Let us consider a charged particle of charge q and mass m moving with velocity $\to v .$ inside a uniform mangetic field $\to B$ making an angle $θ$ wth the direction of magnetic field as shown in then, the valocity $\to v$ can be resolved into the two rectangular components (i) ${\to v}_{1} = v cos θ .$ In the direction of mangetic field and (ii) ${\to v}_{2} = v sin θ .$ in the direction of perpendicular to the magnetic field. Thus, under the effect of two components of velcity, force acting on charged particle is
(i) for $θ = 90^{\circ} .$
Force acting on the charged particle due to magnetic field for compnent ${\to v}_{2}$ is given by :
$\to F = q ({\to v}_{2} \times \to B) or \to F = q v_{2} B {sin 90}^{\circ}$
$= q = v_{2} B$
or $\to F = q (v sin θ) B$
Thus force $\to F$ is acting perpendicular to the plane of ${\to v}_{2} and \to B,$ so it will simply move the particle in circle and provides the necessary centripital force.
If r is the radius of the circular path. then
$v (v sin θ) B = \frac{m v_{2}^{2}}{r}$
or $q (v sin θ) B = \frac{m v^{2} {sin}^{2} θ}{r} or v sin θ = \frac{q r B}{m}$
$∴$ Time period,
$T = \frac{2 π r}{v_{2}} = \frac{2 π r}{v sin θ}$
or $T = \frac{2 π r m}{q r B}$
$or T = \frac{2 π m}{q B}$
And its angular frequency is ,
$ω = \frac{2 π}{T} = \frac{q B}{2 π m}$
(ii) for $θ = 0^{\circ} .$
The force acting on charged particle due to magnetic field for component ${\to v}_{1}$ is given by
${\to F}_{1} = q ({\to v}_{1} \times \to B)$
or $F_{1} = q v_{1} B {sin 90}^{\circ} = 0$
So, the charged particle will cover linear distance in the direction of magnetic field with same passed $v = v_{1} cos θ .$
Thus, charged particle will cover circular as wll as linear path, under the effect of two component of velocity . i.e., helical path whose axis is parallel to the magnetic field as shown in
Pitch of Helix : It is the linear distance covered by the charged particle in magnetic field during time equa to its period.
$∴ S = v_{1} T = \frac{v cos θ 2 π m}{q B}$

Updated on:21/07/2023