Question

Find an expression for angular frequency when charged particle moves at right angle to the magnetic field ?

Explanation

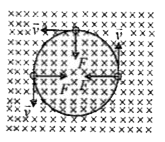
Consider a charged particle q enters the region of magnetic field having velocity `vec v` perpendicular to the direction of magnetic field.
Now force acting on the charge q due to magnetic field `vec B` is
`|vecF| = | q (vec v xx vec B) | = q v B sin theta `
`F = q v B sin 90^(@) = q v B [ because theta = 90^(@) ]" "...(i)`
This force is always normal to the magnetic field and firection of motion. Thus the path of the charged particle is circular.
`therefore ( mv ^(2))/( r ) = q v B`
`implies r = ( mv )/( q B) " "...(ii)`
Thus equation (ii) gives the radius of the circular path.
`therefore ` Time period `(T) = ("Distance")("Speed") = ( 2 pi r )/(v) ...(iii)`
Subsituting equation (ii) in (iii) we get

`T = ( 2pi )/(v) xx (mv)/( q B) = ( 2pi m )/( q B) ...(iv)`
Hence frequency `u = (l)/(T) = ( q B)/( 2 pi m ) ....(v)`
Thus, angular frequency is given by
`omega = ( 2 pi )/(T) = 2 pi u = 2pi xx ( q B)/( 2 pi m ) implies omega = ( q B)/( m ) ....(vi)`