क्या एक ऐसे फलन का अस्तित्व है , जो प्रत्येक बिंदु पर संतत हो किन्तु केवल दो बिंदुओं पर अवकलनीय न हो ? अपने उत्तर का ओचित्ये भी बतलाइये ।
Step by step video & image solution for क्या एक ऐसे फलन का अस्तित्व है , जो प्रत्येक बिंदु पर संतत हो किन्तु केवल दो बिंदुओं पर अवकलनीय न हो ? अपने उत्तर का ओचित्ये भी बतलाइये । by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- अवकलनीयताBOOK - SBPD PUBLICATIONCHAPTER - अवकलनीयताEXERCISE - एन.सी.ई.आर.टी. एक्सेम्पलर(सत्य/असत्य छाँटिये)
1 Videos
- अवकलनीयताBOOK - SBPD PUBLICATIONCHAPTER - अवकलनीयताEXERCISE - उच्च स्तरीय बुद्धि कौशल प्रश्न
1 Videos
- अवकलनीयताBOOK - SBPD PUBLICATIONCHAPTER - अवकलनीयताEXERCISE - एन.सी.ई.आर.टी. एक्सेम्पलर (वस्तुनिष्ठ प्रश्न)
3 Videos
- अवकलनBOOK - SBPD PUBLICATIONCHAPTER - अवकलनEXERCISE - कम्प्टीशन कॉर्नर
2 Videos
- आव्यूह BOOK - SBPD PUBLICATIONCHAPTER - आव्यूह EXERCISE - कम्प्टीशन कॉर्नर
3 Videos
Similar Questions
त्रिकोणमितीय एवं त्रिकोणमितीय व्युत्क्रम फलन अपने-अपने प्राँतों में अवकलनीय होते हैं।
View Solutionदर्शाइए कि फलन f(x)=(x−a)m(x−b)n, जहाँ m,n धनात्मक पूर्णांक है, रोले प्रमेय को अंतराल [a,b] पर सन्तुष्ट करता है।
View Solutionबिंदुओं का वह समुच्चय, जाहाँ f(x)=|2x−1|sinx से दिये जाना वाला फलन f अवकलनीय है, निम्नलिखित है
View Solutionयदि x∈(0,14) के लिए tan−1(6x√x1−9x3) का अवकलन √x.g(x) है, तो g(x) बराबर है
View Solutionनिम्न में से कौन-सा ( से) वास्तविक संख्याओं के 3×3 आव्यूह का वर्ग नहीं है ( हैं) ?
View Solutionनिम्नलिखित कथनो में से सत्य असत्य लिखिए और अपने उत्तर का औचित्य भी दीजिए।
किसी रेखा से समान दूरी पर स्तिथ बिन्दुओ का समुच्चय एक रेखा होती है।
View Solutionनिम्नलिखित कथनो में से सत्य असत्य लिखिए और अपने उत्तर का औचित्य भी दीजिए।
एक वृत्त उन बिन्दुओ का बिन्दुपथ है जो किसी दिए गए बिंदु से नियत दूरी पर स्तिथ है।
View Solutionनिम्न में से प्रत्येक कथन सत्य या असत्य है लिखिए और उत्तर का कारण भी लिखिए।
किसी वृत्त की स्पर्श रेखा वह है जो वृत्त को दो बिंदु पर प्रतिच्छेद करती है।
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
View Solutionकिसी बिन्दु पर संतत फलन होता है -
View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
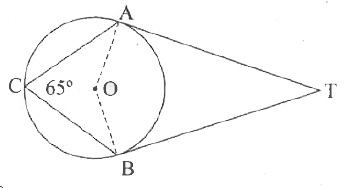
View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -

View Solutionनिम्न कथन सत्य है अथवा असत्य-
यदि सुसंगत क्षेत्र के दो कोनीय बिंदुओं पर इष्टतमकारी मान समान हो अर्थात दोनों बिंदुओं के लिए उद्देश्य फलन का मान या तो उच्चतम या निम्नतम हो तब इन बिंदुओं को मिलाने वाली रेखा पर किसी भी बिंदु के लिए उद्देश्य फलन का इष्टतमकारी मान प्राप्त होता है।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
यदि कोई ऐसे बिंदु निश्चित करना संभव न हो, जहाँ समस्या का अनुकूलतम हल हो, तो समस्या का हल अपरिवद्ध होता है।
View Solutionमाना O(0,0) तथा A(0,1) दो निश्चित बिंदु है, तो ऐसे बिंदु P जिनके लिए ΔAOP का परिमाप 4 हो, का बिन्दुपथ है
View Solution
