Derive an expression for the capacitance of a parallel plate capacitor with dielectric as the medium between the plates.Solution in Punjabi
Capacitor : An arrangement of two metallic conductors separated by some non conducting medium which can store large amount of charge in small space is called a capacitor.
Capacitor is also known as a condenser.
C0=ε0Ad,
Di-electrics : Those non-conducting materials in which equal and opposite induced charges are produced on their opposite faces, when electric field is applied, are called dielectrics.
Capacitance of a parallel plate capacitor having vacuum (or air) between the plates of the capacitor is given by-
C0=ε0Ad,
where A - Area of each plate
d = Distance or separation between the plates of a capacitor
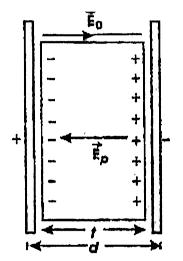
Now, let us introduce a dielectric slab of thickness .t. between the plates of the capacitor.
Due to polarization, equal and opposite induced charges appear on the two faces of the dielectric slab. These induced charges give rise to induced electric field (−→Ep) which is in a direction opposite to the applied field (→E0). The reduced
value of the electric field in the dielectric, E=(E0−Ep).
Now, E=(E0−Ep) exists in a region of thickness .t. and E0 field exists in a region of thickness (d - t).
Potential difference between the two plates of the capacitor
is given by:
V=E0(d−t)+ET
Since, E0E=K or E=E0K
∴V=E0(d−t)+E0Kt=E0[(d−t)+tK]......(2)
We know, E0=σε0=qAε0 [∴σ=q/A]
∴ Eqn (2) becomes V=qAε0[(d−t)+tK]......(3)
Now, Capacitance of the capacitor
C=qV=qAε0q[(d−t)+tK] or C=ε0A(d−t)+tK
C=C01−td(1−1K)
Clearly, C>C0
So when a dielectric slab is introduced.between the plates of a parallel plate capacitor, then its capacity increases.
If the dielectric fills the whole space between the plates of a capacitor i.e., t = d
Then C=C01/K=KC0
The capacity of a capacitor increases by dielectric constant (K) times.
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CAPACITANCE EXERCISE - LONG ANSWERTYPE QUESTIONS (5/6 Marks Questions)16videos
CAPACITANCE
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CAPACITANCE EXERCISE - NUMERICAL PROBLEMS21videos
CAPACITANCE
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CAPACITANCE EXERCISE - SHORT ANSWERTYPE QUESTIONS (2 Marks Questions)5videos
CAPACITANCE
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ALTERNATING CURRENTS EXERCISE - MOST EXPECTED QUESTIONS11videos
ALTERNATING CURRENTS
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - CLASSIFICATION OF MATERIALSEXERCISE - Most expected question (2 marks)3videos
CLASSIFICATION OF MATERIALS
Similar Questions
Derive an expression for capacitance of a parallel plate capacitor.
03:35View SolutionA parallel plate capacitor with air between the plates has a capacitance of 8 pF. The separation between the plates is now reduced by half and the space between them is filled with a medium of dielectric constant K. Calculate the value of the capacitance of the capacitor in the second case.
08:42View SolutionFind an expression for the capacity of a metallic sphere.
04:03View SolutionWhat is a phasor?
06:32View SolutionDoes the magnetisation of a paramagnetic salt dependon temperature ? Give reason for your answer.
06:35View SolutionDerive an expression for the capacitance of a parallel-plate capacitor filled with a dielectric.
06:40View Solutionसमान्तर पट्ट संधारित्र की धारिता के लिए व्यजंक ज्ञात कीजिए जबकि पट्टों के मध्य आंशिक रूप से परावैद्युत माध्यम स्थित हो |
02:03View Solutionसमांतर प्लेट संधारित्र की धारिता के लिए व्यंजक ज्ञात कीजिये जबकि प्लेटो के मध्य आंशिक परावैद्युत माध्यम स्थित हो।
06:40View Solutionपरावैद्युत क्या है? समांतर प्लेट संधारित्र की प्लेटों के बीच परावैद्युत माध्यम डालने पर उसकी धारिता क्यों बढ़ जाती है ? ऐसे समांतर प्लेट संधारित्र की धारिता हेतु व्यंजक व्युत्पन्न कीजिए जिसकी समरूप प्लेटों में से प्रत्येक का क्षेत्रफल A, उनके बीच की दूरी x तथा उनके बीच K परावैद्युतांक का माध्यम भरा हुआ है|
View SolutionBriefly explain the principle of a capacitor. Derive an expression for the capacitance of a parallel plate capacitor, whose plates are separated by a dielectric medium.
06:08View SolutionDefine capacitance of a parallel plate capacitor,Derive an expression for the capacitance of a parallel plate capacitor with dielectric of thickness "t," where "(t
02:43View SolutionCompare the capacitance of a parallel plate capacitor with and without the dielectric medium.
10:03View SolutionDerive a relation for capacitance of a parallel plate capacitor with dielectric slab of thickness t filled between the plates. Or. Write expression for capacitance of a parallel plate capacitor and explain the effect of dielectrics on capacitance.
View SolutionDerive an expression for the capacitance of a parallel plate capacitor. Explain the effect of dielectrics on capacitance of this capacitor. Or. Derive expression for capacitance of a parallel plate capacitor. Explain the effect of dielectrics on its capacitance.
04:16View SolutionDerive an expression for the capacitance of a parallel plate capacitor with dielectric as the medium between the plates.
05:31View SolutionDerive an expression for capacitance of a parallel plate capacitor.
04:32View Solution

