Question

Explain the construction and working of an astronomical telescope. find an expression for its magnifying power in normal adjustment.

Explanation

Telescope. A telescope is an optical instrument used for observing distant objects very clearly.
Astronomical telescope. It produces virtual and inverted image and is used to see heavenly bodies like the sun, stars, planets etc. So the inverted image does not affect the observation.
Principle. It is based on the principle that when rays of light are made to incident on objective from a distant object, the objective forms the real and inverted image at its focal plane. The eye lens is so adjusted that the final image is formed at least distnace of distinct vision or at infinity (normal adjustment).
Construction. The refracting type astronomical telescope consists of two convex lenses one of which is called the objective and the other eye piece. The objective is a convex lens of large focal length and large aperture. It is generally a combination of two lenses in contact so as to reduce spherical and chromatic aberrations. The epe piece is also a convex lens but of short focal length and small aperture. The objective is mounted at one end of a brass tube, and the eye piece at the other end is a smaller tube which can slide inside the bigger tube carrying the objective.

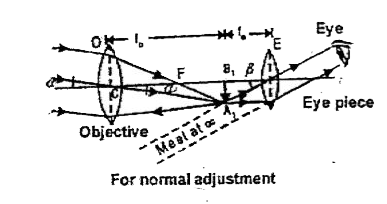
When the final image is formed at infinity. The distance between the image `A_(1),B_(1)` and the eye piece is adjusted equal to the focal length of the eye piece so that the final image is formed at infinity. In this case, telescope is said to be in normal adjustment or focussed to infinity. In normal adjustment, distance between two lenses `=(f_(o)+f_(e ))`.
The magnifying power of a telescope in normal adjustment is defined as the ratio of the angle subtended by the image at the eye as seen through the telescope to the angle subtended by the object at the unaided eye, the object and the image both lying at infinity.
Let `" " angleA_(1)CB_(1)=alpha=` Angle subtended by object at eye/eye piece
and `" "angleB_(1)C_(1)A=beta=` Angle subtended by the image at eye
Magnifying power `= M = (beta)/(alpha)`
If `alpha` and `beta` are small angles then
`M=(tan beta)/(tan alpha)=(A_(1)B_(1))/(B_(1)C_(1)) xx (B_(1)C)/(A_(1)B_(1))`
`M=(B_(1)C)/(B_(1)C_(1))`
When the rays emerging from the eye piece are parallel, the image `A_(2)B_(2)` lies at infinity and distance `B_(1)C_(1)` is equal to focal length of eye piece `(-f_(e ))`.
Also the distance `B_(1)C=f_(o)=` Focal length of the objective lens.
Magnifying power `=(B_(1)C)/(B_(1)C_(1))= -(f_(o))/(f_(e ))`
`M=(f_(o))/(f_(e ))` When final image is formed at least distance of distinct vision :
When a parallel beam of light rays from the distant object falls on the objective, its real and inverted image A, B is formed on the other side of the objective. The position of eyepiece is adjusted so that the final image `A_(1)B_(1)` is formed at least distance of distinct vision. The course of the rays will be as shown in Fig.

Magnifying power. Magnifying power telescope is defined as the ratio of the angle subtended at the eye by. the image formed at the least distance of distinct vision to angle subtended at the eye by the object lying at infinity, when seen directly.
Again, as the object is at very large distance, the angle a suhtended by it at the objective is practically the same as that subtended by it at the eye. Therefore, if `angle A..CB.=beta` then
`M=(beta)/(alpha)`
Again, as angles `alpha` and `beta` are small, they can be replaced by their tangents, Therefore,
`M=(tan beta)/(tan alpha)" "...(i)`
From right angled `DeltaCA.B, tan alpha=(A_(1)B_(1))/(CB_(1))`
and from right angled `DeltaCA.B., tan beta=(A_(1)B_(1))/(C_(1)B_(1))`
In equation (i), substituting for `tan alpha tan beta`, we have
`M=(A_(1)B_(1)//C_(1)B_(1))/(A_(1)B_(1)//C_(1)B_(1))=(CB_(1))/(C_(1)B_(1))" "...(ii)`
In equation (ii), subsituting for `CB_(1)` and `C_(1)B_(1)`, we get
`M=(f_(0))/(u_(e )) " " ...(iii)`
For eye lens, we have
`-(1)/(u_(e )) +(1)/(v_(e ))=(1)/(f_(e )) or (1)/(v_(e ))=(1)/(f_(e ))+(1)/(v_(e ))`
or `(1)/(u_(e ))= -(1)/(f_(e )) (1-(f_(e ))/(v_(e )))`
Substituting for `(1)/(u_(e ))` in equation (iii), we have
`M= -(f_(o))/(f_(e ))(1-(f_(e ))/(v_(e )))`
Applying new cartesian sign conventions :
`f_(o)= +f_(o), v_(e )= -D, f_(e )= +f_(e )`
`M= -(f_(o))/(f_(e )) (1-(f_(e ))/((-D)))`
`M= -(f_(o))/(f_(e )) (1+(f_(e ))/(D))`