Explain various energy bands in an atom.Solution in Punjabi
In order to understand as to how the energy levels get modified, consider a single small crystal of silicon made of N atom. An atom of silicon has electronic configuration 1s2,2s2,2p6,3s2,3p2. The various energy levels of silicon atom can be represented as shown in Fig. The outermost shell contains 2 electrons in 3s subshell and 2 electrons in 3p subshell. The 3s levels (all of the same energy) in the outermost shells of all the N atoms, which are 2N in number are completely filled by 2N electrons, while out of total 6N p-levels (all of the same energy) in the outermost shells of N atoms, only 2N are filled.

Suppose that the interatomic separation between the silicon atoms in the crystal lattice is a and these atoms are brought from the locations r>>a to their actual location r=a by gradually moving the atoms towards each other.
(i) When r=d1. At this interatomic separation, electrons in the outermost shell of one atom do not ineract with those of the other. Therefore, at r=d1, each of N atoms has its own typical energy levels i.e., energy levels 1s2,2s2,2p5,3s2,3p6 of each atom remain unmodified.
(ii) When r=d2, When the interatomic separation is decreased from r=d1 to r=d2, the interaction between the electrons of different atoms in the outermost shells (3s2and3p2) begins. Due to this, the energy of 3s and 3p levels of each atom gets slightly modified, when they are at distance r=d2. Therefore, instead of a single 3s and 3 p-level, there occur a large number of closely spaced energy levels. Now, the 2N s-levels will not have same energy but will be spread in small energy band. Similarly, 6N p-levels will also be spread into a small energy band. Due to this, the energy gap between s and p-levels of an isolated atom reduces.
(iii) When r=a. When the silicon atoms are the actual interatomic separation a, the energy of the band of 8 N levels splits into two bands, band of 4N energy levels completely filled with electrons and another band of 4 N empty levels. These two energy bands are separated from each other with a small energy gap. The lower energy band of 4 N filled levels is called the valence band, while the upper energy band of 4 N empty levels is called the conduction band. The energy gap between the valence band and the conduction band is called the forbidden energy gap.
(a) Metals: The energy band structure in solids have two possibilities:
(i) The valence band may be completely filled and the conduction band partially filled with an extremely small energy gap between them (Fig). For example, in sodium, the conduction band is partially filled, while the valence band is completely filled.

(ii) The valence band is completely filled and the conduction band is empty but the two overlap each other (Fig). Zinc is an example of band overlap metals. In both the situations, it can be assumed that there is a single energy band, which is partially filled. Therefore, on applying even a small electric field, the metals conduct electricity.
(b) Insulators, In insulators, the forbidden energy gap is quite large (see Fig) For example, the forbidden energy gap for diamond is 6 eV, which means that a minimum of 6eV energy is required to make the electron jump from the completely filled valenced band to the conduction band. When electric field is applied across such a solid, the electrons find it difficult to acquire such a large amount of energy and so the conduction band continues to be almost empty. No electron flow occurs i.e., no current flows through such solids. So they behave as insulators.

(c ) Semiconductors. The energy band structure of the semiconductors is similar to the insulators but in their case, the size of the forbidden energy gap is much smaller than that for the insulators (See Fig). For example, the forbidden band for silicon 1.1eV. The electronic structure of the silicon (Si) is similar to that of the diamond, but due to the smaller width of the forbidden energy gap, the electrons in the valence band find it comparatively easier to shift to the conduction band. So, the conductivity of the silicon is in between the conductors and the insulators and it is termed as a semiconductor.
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRONIC DEVICES SOLIDSEXERCISE - Long Answer Type Questions2videos
ELECTRONIC DEVICES SOLIDS
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRONIC DEVICES SOLIDSEXERCISE - Numerical Problems7videos
ELECTRONIC DEVICES SOLIDS
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRONIC DEVICES SOLIDSEXERCISE - Most Expected Questions9videos
ELECTRONIC DEVICES SOLIDS
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - NUMERICALS4videos
ELECTROMAGNETIC WAVES
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - NUMERICAL PROBLEMS (MOST EXPECTED QUESTIONS)6videos
ELECTROSTATIC POTENTIAL
Similar Questions
Explain the behaviour of semiconductors and insulators on the basis of energy bands in solids.
03:23View SolutionA semiconductor has accpetor level 1.57 eV above the valence band.What is the maximum wavelength of light required to create a hole?Given that 1eV=1.6×10−19J and h=6.62×10−34Js.
06:31View SolutionWhy semiconductors are doped?
06:43View SolutionFind the wavelength of electromagnetic waves of frequecies 4×1017 Hz in free space.Give its two applications.
07:31View SolutionCalculate the electric potential at the surface of a gold nucleus. Given radius of nucleus = 6.6×10−15m and atomic wight of gold is 79.
03:42View Solutionऊर्जा स्तर और ऊर्जा बैण्ड में अन्तर बताइये।
03:06View SolutionP- प्रकार के अर्द्धचालक को ऊर्जा बैण्ड के पदों में समझाइए।
04:37View Solutionn- प्रकार के अर्द्धचालक को ऊर्जा बैण्ड के पदों में समझाइए।
03:20View Solutionऊर्जा बैंड की अवधारणा को चित्र सहित समझाइये|
11:36View SolutionExplain the .Conduction band. .Valence band. and .Energy gap. in semiconductors.
03:42View SolutionMention the various energy losses in a transformer.
01:28View SolutionWhat are energy bands ? Explain the formation of energy bands in case of silicon crystal.
04:42View SolutionWrite a note on transformer.
03:42View Solutionव्याख्या करें कि हम ठोस पदार्थों में ऊर्जा बैंड कैसे प्राप्त करते हैं। अपने ऊर्जा बैंड चित्र के आधार पर ठोस पदार्थों का वर्गीकरण किस प्रकार किया जाता है ?
06:01View SolutionExplain the .Conduction band. .Valence band. and .Energy gap. in semiconductors.
View Solution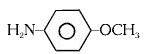
का IUPAC नाम है :-View Solution

