Comprehension 3 x+y+3z=42x+py+6z=8x+2y+qz=5 Values of p & q for which the system has infinitely many solution a. p≠2, q∈R b. p=2, q∈R c.p∈R, q=3 d. p∈R,\ q≠3
To solve the problem of finding the values of p and q for which the system of equations has infinitely many solutions, we need to analyze the given equations:
1. x+y+3z=4 (Equation 1)
2. 2x+py+6z=8 (Equation 2)
3. x+2y+qz=5 (Equation 3)
For a system of linear equations to have infinitely many solutions, the equations must be dependent. This means that one equation can be expressed as a linear combination of the others.
Step 1: Write the equations in matrix form
We can represent the system of equations in the form of an augmented matrix:
⎡⎢⎣113|42p6|812q|5⎤⎥⎦
Step 2: Find the determinant of the coefficient matrix
The coefficient matrix is:
⎡⎢⎣1132p612q⎤⎥⎦
To find the determinant, we can use the formula for a 3x3 matrix:
det=a(ei−fh)−b(di−fg)+c(dh−eg)
Where a,b,c,d,e,f,g,h,i are the elements of the matrix:
det=1(p⋅q−6⋅2)−1(2⋅q−6⋅1)+3(2⋅2−p⋅1)
Calculating this gives:
det=pq−12−(2q−6)+3(4−p)
Simplifying this:
det=pq−12−2q+6+12−3p
Combining like terms:
det=pq−2q−3p+6
Step 3: Set the determinant to zero
For the system to have infinitely many solutions, we set the determinant equal to zero:
pq−2q−3p+6=0
Step 4: Analyze the equation
Rearranging gives us:
pq−2q−3p+6=0
This is a linear equation in terms of p and q. To find the values of p and q that satisfy this equation, we can analyze it for different cases.
Step 5: Determine values of p and q
1. If p=2:
2q−2q−6+6=0⟹0=0(True for all q)
Thus, p=2 and q can be any real number.
2. If p≠2:
We can express q in terms of p:
q=3p−6p−2
This means q can take on values depending on p, but p cannot be equal to 2.
Conclusion
Thus, the values of p and q for which the system has infinitely many solutions are:
- p=2 and q∈R (Option b)
- p≠2 and q can be any real number (Option a)
Final Answer
The correct options are:
- Option a: p≠2,q∈R
- Option b: p=2,q∈R
2. 2x+py+6z=8 (Equation 2)
3. x+2y+qz=5 (Equation 3)
2q−2q−6+6=0⟹0=0(True for all q)
Thus, p=2 and q can be any real number.
We can express q in terms of p:
q=3p−6p−2
This means q can take on values depending on p, but p cannot be equal to 2.
- p≠2 and q can be any real number (Option a)
- Option a: p≠2,q∈R
- Option b: p=2,q∈R
Topper's Solved these Questions
Similar Questions
For what values of p and q the system of equations 2x+py+6z=8,x+2y+qz=5,x+y+3z=4 has no solution. (a).p=2,q≠3. (b).p≠2,q≠3 (c). p≠2,q=3 (d). p=2,q=3
View SolutionFind the values of p and q for which the following system of equations has infinite number of solutions: 2x+3y=7, (p+q)x+(2p−q)y=21
View Solution
Knowledge Check
In Figure 1, y=√3xandz=2x. What is the ratio p:q:r in figure 2?
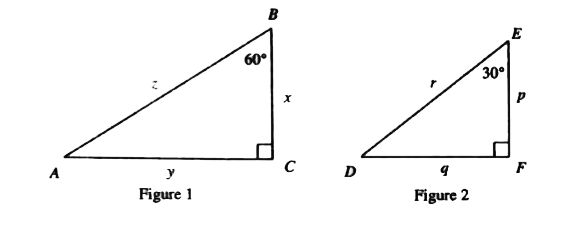 A1:2:3B√3:1:2C1:√3/2:1D2:√3:1
A1:2:3B√3:1:2C1:√3/2:1D2:√3:1If p=√q+zr2+z, what is the value of z in terms of p, q, and r ?
Ap−r2√qp−1Bpr2−√qr2C√p+qrr2D√q−pr2p−1
Find the values of p and q for which the following system of equations has infinite number of solutions: 2x+3y=7, (p+q)x+(2p−q)y=21
View SolutionFor what values of p and q the system of equations 2x+py+6z=8,x+2y+qz=5,x+y+3z=4 has a unique solution. (a).p=2,q≠3 (b).p≠2,q≠3 (c).p≠2,q=3 (d).p=2,q=3
View SolutionFind the values of p and q for which the following system of linear equations has infinite number of solutions: 2x+3y=9, (p+q)x+(2p−q)y=3(p+q+1)
View SolutionFor the system of equations x+y+z=4,y+2z=5andx+y+pz=q to have no solution (A) p=1andq=4 (B) p=1andq≠4 (C) p≠1andq=4 (D) p≠1andq≠4
View SolutionFind the value of :
2p + 3q + 4r + por when p =-1,q = 2 and r = 3
View SolutionWrite the coefficient of:
(i)z in −7xyz
(ii) p in −3pqr
View Solution
