In a triangle ABC , if B=300and c=√3 b, then A can be equal to (a)450 (b) 600 (c) 900 (d) 1200
To solve the problem step by step, we will use the properties of triangles and the sine rule.
1. Identify the Given Information:
We are given:
- Angle B=30∘
- Side c=√3b
2. Apply the Sine Rule:
The sine rule states that:
sinAa=sinBb=sinCc
From the information given, we can set up the following relationship:
sinBb=sinCc
Substituting the values we have:
sin30∘b=sinC√3b
3. Simplify the Equation:
Since b appears in both denominators, we can cancel it out:
sin30∘1=sinC√3
We know that sin30∘=12, so:
12=sinC√3
4. Cross-Multiply to Solve for sinC:
Cross-multiplying gives us:
sinC=12⋅√3
Thus:
sinC=√32
5. Determine the Value of Angle C:
The angle C for which sinC=√32 is:
C=60∘
6. Use the Triangle Sum Property:
The sum of angles in a triangle is 180∘:
A+B+C=180∘
Substituting the known values:
A+30∘+60∘=180∘
7. Solve for Angle A:
A+90∘=180∘
Therefore:
A=180∘−90∘=90∘
8. Conclusion:
The value of angle A can be equal to 90∘. Thus, the correct option is:
(c) 90°
We are given:
- Angle B=30∘
- Side c=√3b
The sine rule states that:
sinAa=sinBb=sinCc
From the information given, we can set up the following relationship:
sinBb=sinCc
Substituting the values we have:
sin30∘b=sinC√3b
Since b appears in both denominators, we can cancel it out:
sin30∘1=sinC√3
We know that sin30∘=12, so:
12=sinC√3
Cross-multiplying gives us:
sinC=12⋅√3
Thus:
sinC=√32
The angle C for which sinC=√32 is:
C=60∘
The sum of angles in a triangle is 180∘:
A+B+C=180∘
Substituting the known values:
A+30∘+60∘=180∘
A+90∘=180∘
Therefore:
A=180∘−90∘=90∘
The value of angle A can be equal to 90∘. Thus, the correct option is:
(c) 90°
Topper's Solved these Questions
Similar Questions
In a triangle ABC,∠A=600andb:c=(√3+1):2, then find the value of (∠B−∠C).
View SolutionIn the figure, if AB=AC,∠BAD=300 and AE=AD, then x is equal to
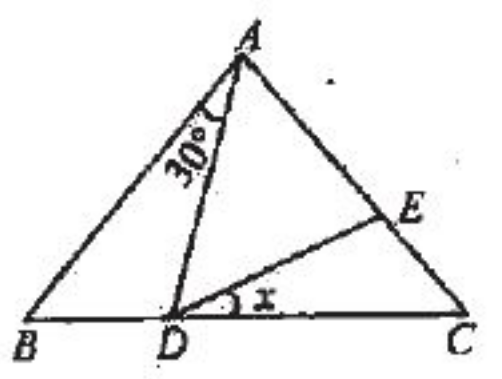
a)150 (b) 100 (c) 12.50 (d) 7.50View SolutionAn equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOC is
View SolutionIn a parallelogram ABCD , if ∠DAB=750and ∠DBC=600, then ∠BDC=(a) 750 (b) 600 (c) 450 (d) 550
View SolutionIn a parallelogram ABCD , if ∠DAB=750and ∠DBC=600, then ∠BDC= (a) 750 (b) 600 (c) 450 (d) 550
View SolutionIf an a triangle ABC,b=3c,and C−B=900, then find the value of tanB
View SolutionIf an a triangle ABC,b=3cand C−B=900, then find the value of tanB
View SolutionIn Figure, the value of y is
(a) 200
(b) 300
(c) 450
(d) 600View SolutionThe angles of a triangle are in the ratio 1:2:3. The measure of the largest angle is: (a)300 (b) 600 (c) 900 (d) 1200
View SolutionIn Figure, If ∠ABC=450, then ∠AOC= (a) 450 (b) 600 (c) 750 (d) 900
View Solution

