If In is the area of n sided regular polygon inscribed in a circle of unit radius and On be the area of the polygon circumscribing the given circle, prove that In=On2⎛⎝1+⎛⎝√1−(2Inn)2⎞⎠
Step by step video & image solution for If I_n is the area of n sided regular polygon inscribed in a circle of unit radius and O_n be the area of the polygon circumscribing the given circle, prove that I_n=(O_n)/2(1+(sqrt(1-((2I_n)/n)^2)) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In is the area of n sided refular polygon inscribed in a circle unit radius and On be the area of the polygon circumscribing the given circle, prove that In=On2⎛⎝1+√1−(2Inn)2⎞⎠
View SolutionIf a regular polygon of n sides has circum radius R and inradius r then each side of polygon is:
View SolutionThe ratio of the area of a regular polygon of n sides inscribed in a circle to that of the polygon of same number of sides circumscribing the same is 3:4. Then the value of n is
View SolutionProve that the area of a regular polygon hawing 2n sides, inscribed in a circle, is the geometric mean of the areas of the inscribed and circumscribed polygons of n sides.
View SolutionIf r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
View SolutionThe ratio of the area of a regular polygon of n sides inscribed in a circle to that of the polygon of same number of sides circumscribing the same is 3:4. Then the value of n is 6 (b) 4 (c) 8 (d) 12
View SolutionGiven that the area of a polygon of n sides circumscribed about a circle is to the area of the circumscribed polygon of 2n sides as 3:2 find n.
View SolutionLet An be the area that is outside a n-sided regular polygon and inside its circumscribeing circle. Also Bn is the area inside the polygon and outside the circle inscribed in the polygon. Let R be the radius of the circle circumscribing n-sided polygon. On the basis of above information, answer the equation If n=6 then An is equal to R2(π−√32) (b) R2(2π−6√32) R2(π−√3) (d) R2(2π−3√32)
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
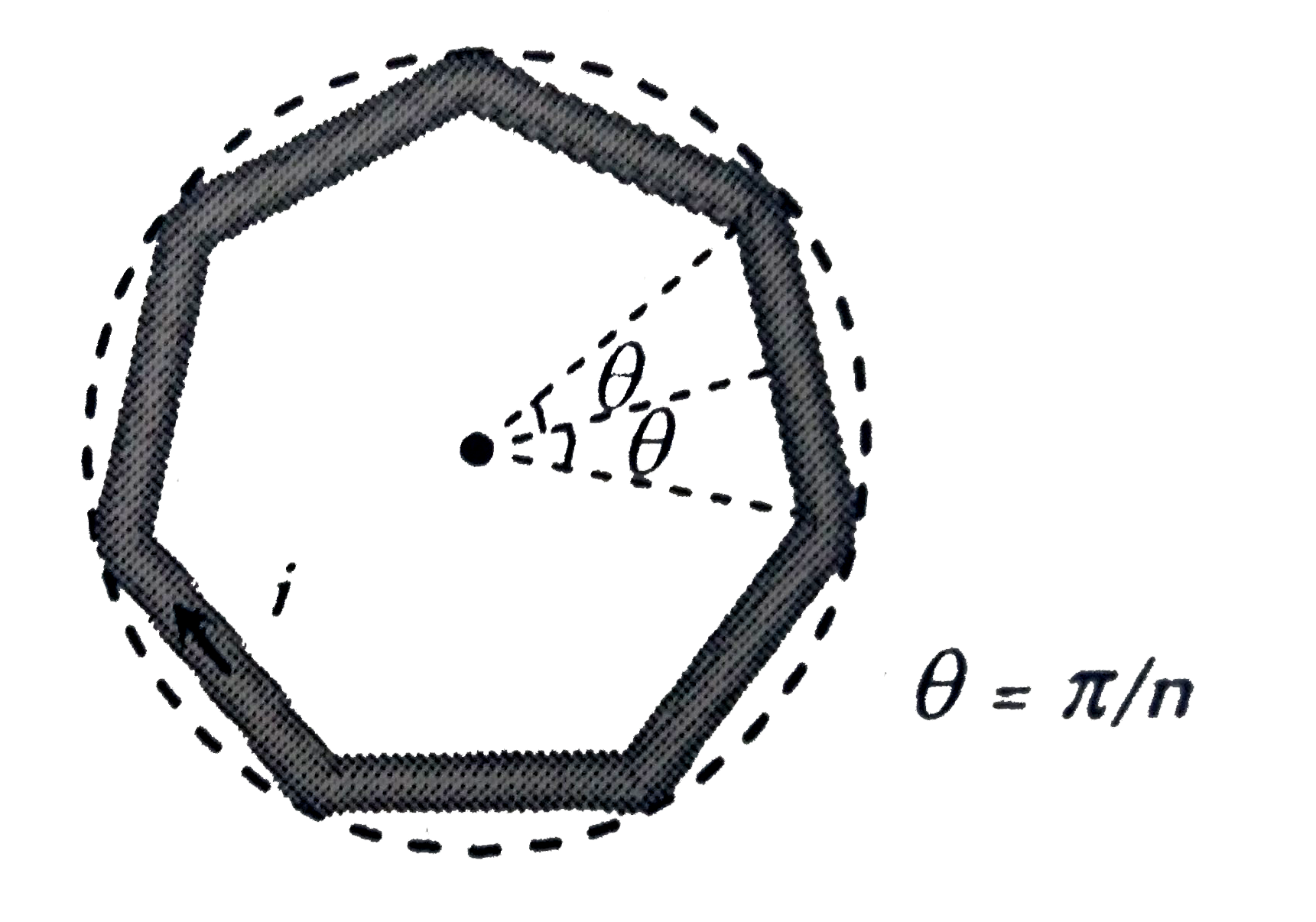
View SolutionThe interior angle of a n sided regular polygon is 48∘ more than the interior angle of a regular hexagon. Find n.
View Solution
