Compare Schrodinger equation with most important equation of Newtions law.
∂2ψ∂x2+∂2ψ∂y2+∂2ψ∂z2=−(E−V)8π2mhψ Schrodinger equation....(i)
md2xdt2=Fm Newton's law ....(ii)
Both involve solution to different equation.
(i) The first equation is time independent. While the second depends upon time.
(ii) The first equation when solved give infinite solution. While second equation gives only one solution
Topper's Solved these Questions
Similar Questions
Knowledge Check
ψ2 means.
Aradial probability densityBprobability densityCalways positive valueD2 & 3The Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Ψ2s=(Z2a0)½(1−Zra0)e−Zra0
The plot of radial probability function 4πr2R2 aganist r will be:
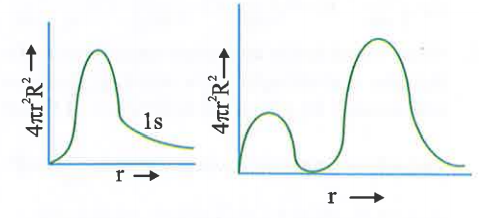
Answer the following questions:
The following graph is plotted for ns-orbitals
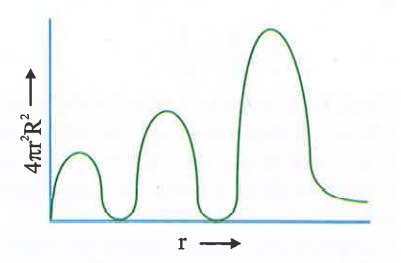
The value of 'n' will be:A1B2C3D4The Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Ψ2s=(Z2a0)½(1−Zra0)e−Zra0
The plot of radial probability function 4πr2R2 aganist r will be:

Answer the following questions:
The value of radius 'r' for 2s atomic orbital of H-atom at which the radial node will exist may be given as:Ar=2a0Br=a04Cr=a0Dr=a05
If y=f(x+ct)+g(x−ct), then show that ∂2y∂t2=c2∂2y∂x2
View SolutionIn schrodinger wave equation ∇2ψ+?π2mh2(E−V)ψ=0 ? is- "
View SolutionShow that the equation,y=asin(ωt−kx) satisfies the wave equation∂2y∂t2=v2∂2y∂x2. Find speed of wave and the direction in which it is travelling.
View SolutionShow that the equation,y=asin(ωt−kx) satisfies the wave equation∂2y∂t2=v2∂2y∂x2. Find speed of wave and the direction in which it is travelling.
View SolutionThe Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Ψ2s=(Z2a0)½(1−Zra0)e−Zra0
The plot of radial probability function 4πr2R2 aganist r will be:

Answer the following questions:
What will be number of angular nodes and spherical nodes for 4f atomic orbitals respectively.
View Solution
