For which orbital angular probability distribution is maximum at an angle of 45∘ to the axial direction ?
dx2−y2
dZ2
dxy
Px
The correct Answer is:C
To determine the orbital angular probability distribution that is maximum at an angle of 45∘ to the axial direction, we need to analyze the angular probability distribution of different orbitals.
1. Understanding Angular Probability Distribution:
The angular probability distribution for an orbital is described by the spherical harmonics Yml(θ,ϕ), where l is the azimuthal quantum number and m is the magnetic quantum number. The angle θ is the polar angle (angle from the z-axis), and ϕ is the azimuthal angle (angle in the xy-plane).
2. Identifying the Angle:
We are interested in the case where the maximum probability occurs at an angle of 45∘ to the axial direction (z-axis). At 45∘, θ=45∘ or θ=π4 radians.
3. Evaluating Different Orbitals:
- For s orbitals (l=0), the probability distribution is spherically symmetric and does not depend on the angle.
- For p orbitals (l=1), the distribution has lobes along the axes (x, y, z) and does not have a maximum at 45∘.
- For d orbitals (l=2), particularly the dxy orbital, the lobes are oriented in the xy-plane and can show significant probability at 45∘ to the z-axis.
4. Conclusion:
The orbital angular probability distribution that has a maximum at an angle of 45∘ to the axial direction is the dxy orbital. This orbital has lobes that extend in the xy-plane, and at 45∘, the probability density is maximized.
Final Answer:
The orbital angular probability distribution that is maximum at an angle of 45∘ to the axial direction is the dxy orbital.
---
The angular probability distribution for an orbital is described by the spherical harmonics Yml(θ,ϕ), where l is the azimuthal quantum number and m is the magnetic quantum number. The angle θ is the polar angle (angle from the z-axis), and ϕ is the azimuthal angle (angle in the xy-plane).
We are interested in the case where the maximum probability occurs at an angle of 45∘ to the axial direction (z-axis). At 45∘, θ=45∘ or θ=π4 radians.
- For s orbitals (l=0), the probability distribution is spherically symmetric and does not depend on the angle.
- For p orbitals (l=1), the distribution has lobes along the axes (x, y, z) and does not have a maximum at 45∘.
- For d orbitals (l=2), particularly the dxy orbital, the lobes are oriented in the xy-plane and can show significant probability at 45∘ to the z-axis.
The orbital angular probability distribution that has a maximum at an angle of 45∘ to the axial direction is the dxy orbital. This orbital has lobes that extend in the xy-plane, and at 45∘, the probability density is maximized.
The orbital angular probability distribution that is maximum at an angle of 45∘ to the axial direction is the dxy orbital.
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 03
21 Videos
- ATOMIC STRUCTUREBOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 04[A]
49 Videos
- ATOMIC STRUCTUREBOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 01
38 Videos
- IUPAC NOMENCLATUREBOOK - ALLENCHAPTER - IUPAC NOMENCLATUREEXERCISE - Exercise - 05(B)
7 Videos
Similar Questions
Knowledge Check
An object is thrown along a direction inclined at an angle of 45∘ with the horizontal direction. The horizontal range of the object is equal to
Avertical heightBtwice the verticalCthrice the vertical heightDfour times the vertical height
Which has maximum bond angle?
View SolutionA particle of mass m collides with a stationary particle and continues to move at an angle of 45∘ with respect to the original direction . The second particle also recoils at an angle of 45∘ to this direction . The mass of the second particle is (collision is elastic )
View SolutionAn object is thrown along a direction inclined at an angle of 45∘ with the horizontal direction. The horizontal range of the particle is equal to
View SolutionWhich of the following probability distribution does not exist for randam variable? Give reason?
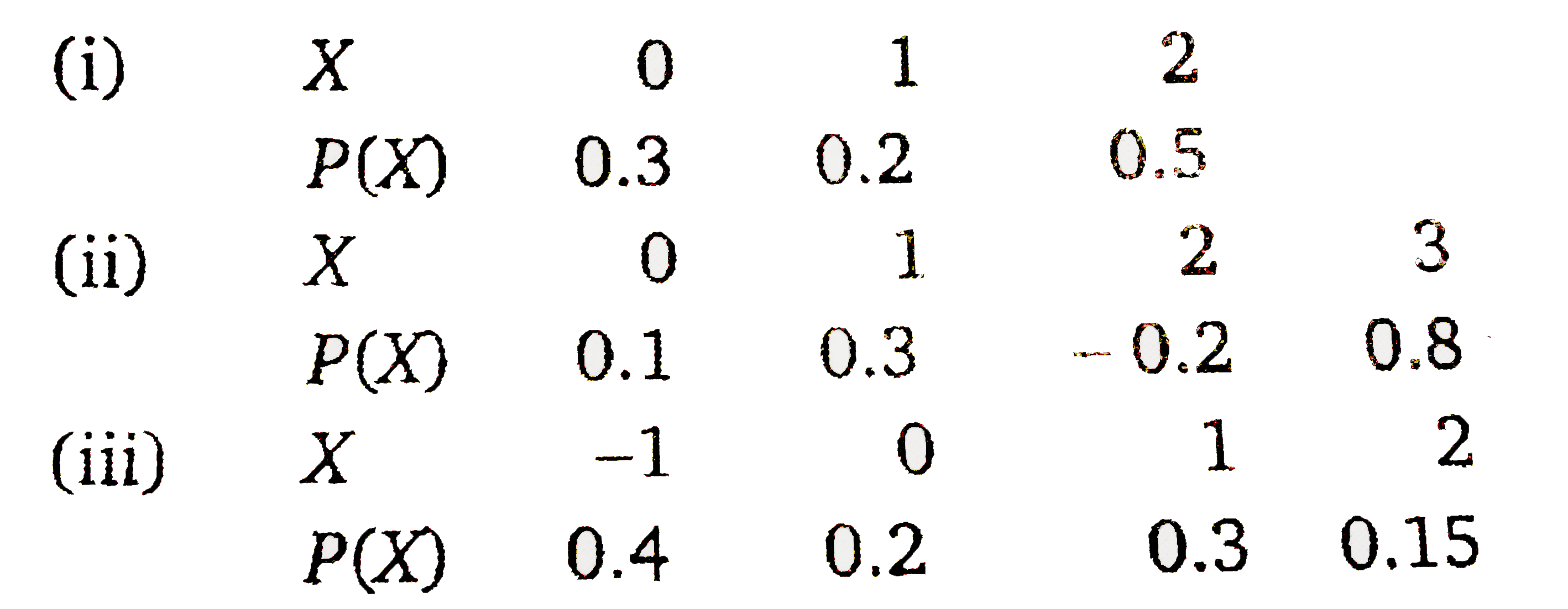
View SolutionA disc of radius R has a light pole fixed perpendicular to the disc at its periphery which in turn has a pendulum of length R attached to its other end as shown in figure. The disc is rotated with a constant angular velocity ω The string is making an angle 45∘ with the rod. Then the angular velocity ω of disc is

View SolutionFind the equation of a line through the origin which makes an angle of 450 with the positive direction of x-axis.
View SolutionA projectile is thrown in the upward direction making an angle of 60∘ with the horizontal direction with a velocity of 150ms−1. Then the time after which its inclination with the horizontal is 45∘ is
View Solution
