The wavelengths of photons emitted by electron transition between two similar leveis in H and He+ are λ1 and λ2 respectively. Then :-
λ2=λ1
λ2=2λ1
λ2=λ1/2
λ2=λ1/4
The correct Answer is:D
To solve the problem regarding the wavelengths of photons emitted by electron transitions in hydrogen (H) and helium ion (He⁺), we need to analyze the energy levels and the relationship between energy and wavelength.
1. Understanding Energy Levels:
The energy of an electron in a hydrogen-like atom is given by the formula:
En=−E1⋅Z2n2
where E1 is the energy of the ground state, Z is the atomic number, and n is the principal quantum number.
2. Energy of Photons:
The energy of a photon emitted during a transition is also related to its wavelength (λ) by the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
3. Relating the Two Atoms:
For hydrogen (H), Z=1 and for helium ion (He⁺), Z=2. Therefore, the energy levels for both can be expressed as:
- For hydrogen:
EHn=−E1⋅12n2=−E1n2
- For helium ion:
EHe+n=−E1⋅22n2=−4E1n2
4. Setting Up the Relationship:
The energy of the emitted photon during a transition can be expressed as:
E=Einitial−Efinal
Therefore, for transitions in hydrogen and helium ion, we can write:
EHphoton=EHnandEHe+photon=EHe+n
5. Finding the Wavelengths:
From the energy-wavelength relationship, we can derive:
λ1∝1EHnandλ2∝1EHe+n
6. Calculating the Ratio of Wavelengths:
The ratio of the wavelengths can be expressed as:
λ2λ1=EHnEHe+n=1222=14
Thus, we can conclude:
λ2=4λ1
Final Result:
The relationship between the wavelengths of photons emitted by electron transitions in hydrogen and helium ion is:
λ2=4λ1
The energy of an electron in a hydrogen-like atom is given by the formula:
En=−E1⋅Z2n2
where E1 is the energy of the ground state, Z is the atomic number, and n is the principal quantum number.
The energy of a photon emitted during a transition is also related to its wavelength (λ) by the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
For hydrogen (H), Z=1 and for helium ion (He⁺), Z=2. Therefore, the energy levels for both can be expressed as:
- For hydrogen:
EHn=−E1⋅12n2=−E1n2
- For helium ion:
EHe+n=−E1⋅22n2=−4E1n2
The energy of the emitted photon during a transition can be expressed as:
E=Einitial−Efinal
Therefore, for transitions in hydrogen and helium ion, we can write:
EHphoton=EHnandEHe+photon=EHe+n
From the energy-wavelength relationship, we can derive:
λ1∝1EHnandλ2∝1EHe+n
The ratio of the wavelengths can be expressed as:
λ2λ1=EHnEHe+n=1222=14
Thus, we can conclude:
λ2=4λ1
The relationship between the wavelengths of photons emitted by electron transitions in hydrogen and helium ion is:
λ2=4λ1
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 0321videos
ATOMIC STRUCTURE
- BOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 04[A]49videos
ATOMIC STRUCTURE
- BOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 0138videos
ATOMIC STRUCTURE
- BOOK - ALLENCHAPTER - IUPAC NOMENCLATUREEXERCISE - Exercise - 05(B)7videos
IUPAC NOMENCLATURE
Similar Questions
A dye absorbs a photon of wavelength λ and re− emits the same energy into two phorons of wavelengths λ1 and λ2 respectively. The wavelength λ is related with λ1 and λ2 as :
View SolutionThe wavelengths and frequencies of photons in transition 1,2 and 3 for hydrogen like atom are λ1,λ2,λ3,v1,v2 and v3 respectively. Then:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The energies E1andE2 of two radiations are 25 eV and 50 eV respectively. The relation between their wavelengths, i.e., λ1andλ2 will be
Aλ1=2λ2Bλ1=4λ2Cλ1=12Dλ1=λ2
Calculate the wavelength of a photon emitted when an electron in H− atom maker a transition from n=2 to n=1
View SolutionThe wavelength of the short radio waves, microwaves, ultraviolet waves are λ1,λ2 and λ3, respectively, Arrange them in decreasing order.
View SolutionIn a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
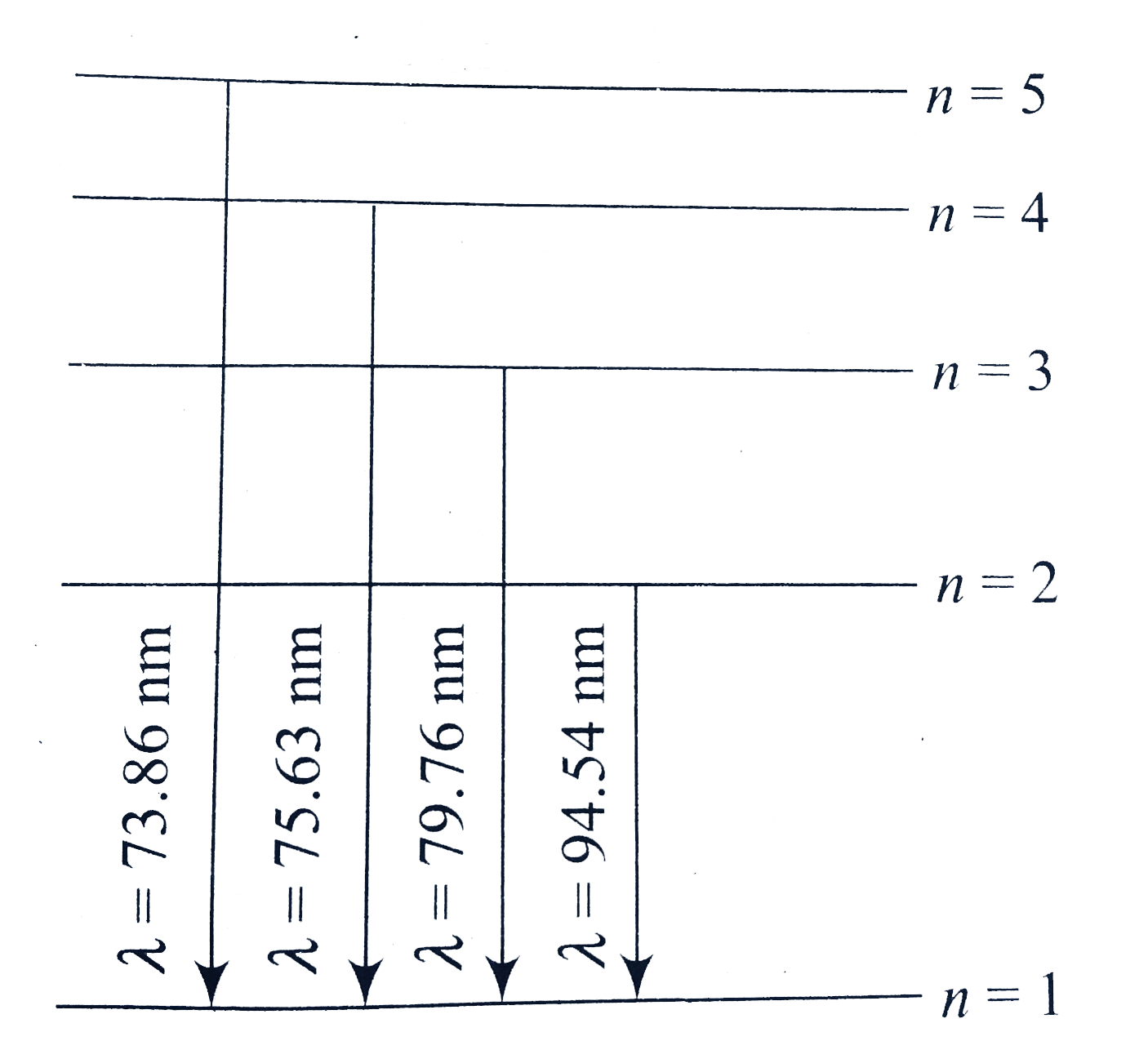
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
If an electron made a transition from n = 4 to n = 2 level, the wavelength of the light that it would emit is nearlyView SolutionIn a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
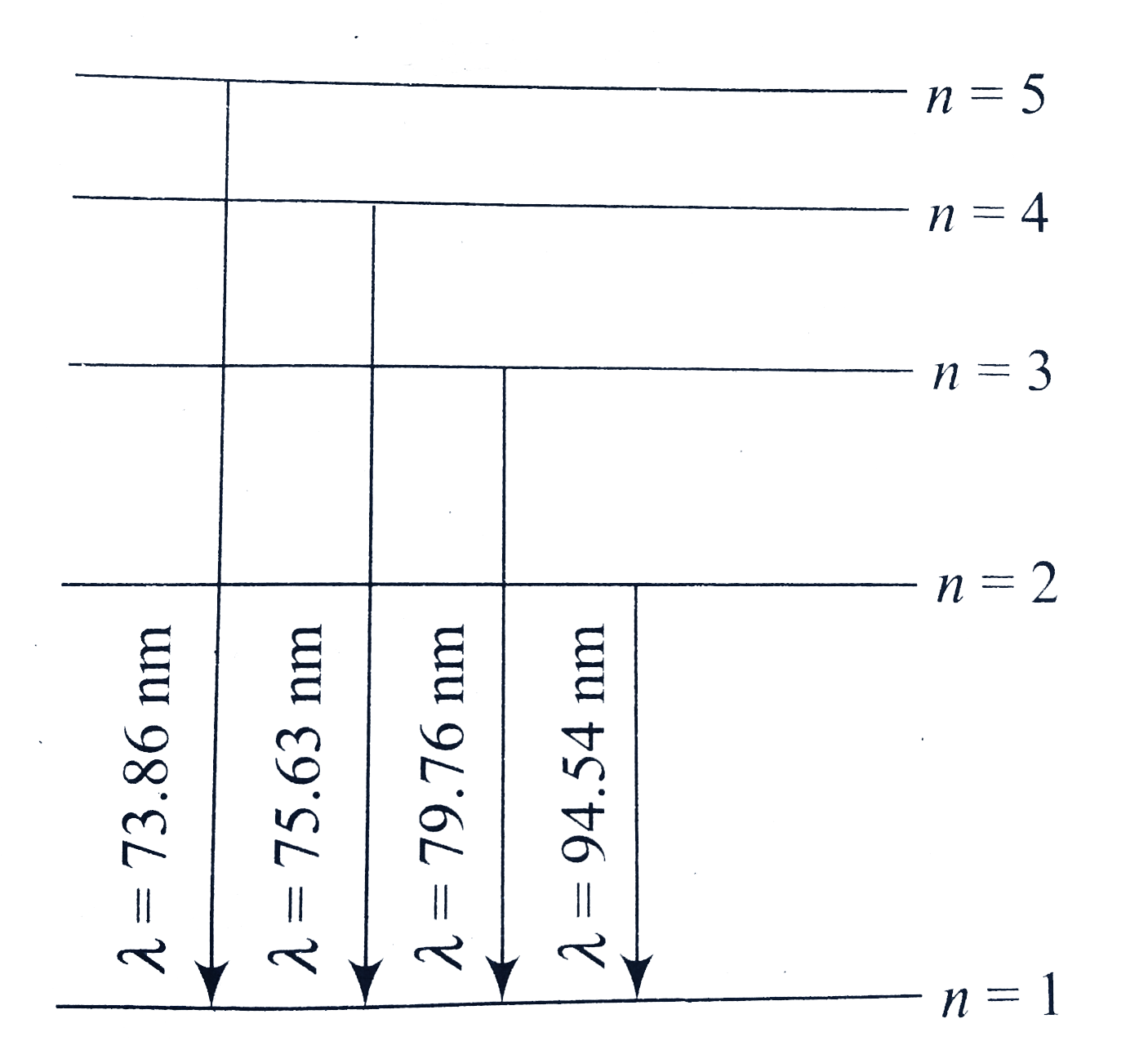
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
The energy of the atom in level n=1 is nearlyView SolutionIn a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
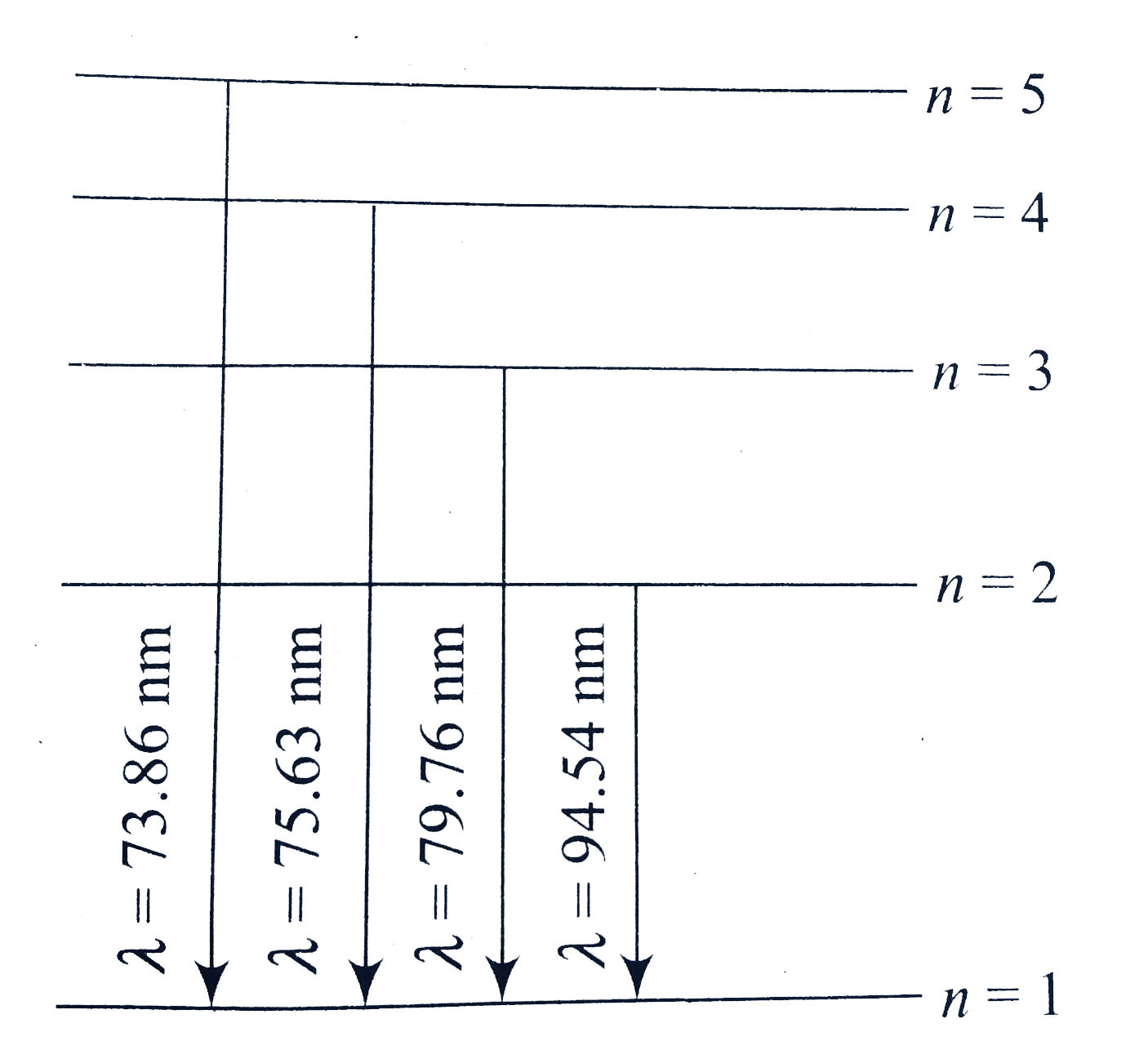
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
The possible energy of the atom in n=3 cannot beView SolutionIf the wavelength of photon emitted due to transition of electron from third orbit to first orbit in a hydrogen atom is λ then the wavelength of photon emitted due to transition of electron from fourth orbit to second orbit will be
View SolutionStatement I : The energy of a He+ ion for a given n is almost exactly four times that of H atom for the same n.
Statement II : Photon emitted during transition between corresponds pair of levels in He+ and H have the same energy E and the same wavelength λ=hc/E.View Solution

