The cell has emf, . The electrode potential for the reaction is volt. Calculate the value:-
The correct Answer is:C
To solve the problem step by step, we will analyze the given electrochemical cell and apply the Nernst equation to find the pH value.
Step 1: Identify the half-reactions
The cell is represented as:
Pt(H2)(1 atm)|H+(pH=?)|AgI(s),Ag
- Anode Reaction: The oxidation reaction at the anode involves hydrogen gas (H2) converting to protons (H+):
H2→2H++2e−
- Cathode Reaction: The reduction reaction at the cathode involves silver iodide (AgI) being reduced to silver (Ag):
AgI+e−→Ag+I−
Step 2: Determine the standard electrode potentials
- The standard electrode potential for the cathode reaction (AgI + e^- → Ag + I^-) is given as:
E∘cathode=−0.151 V
- The standard electrode potential for the anode reaction (standard hydrogen electrode) is:
E∘anode=0 V
Step 3: Calculate the cell EMF
The EMF of the cell is given as:
Ecell=Ecathode+Eanode
Since the EMF is zero:
0=−0.151+Eanode
Thus, we can find Eanode:
Eanode=0.151 V
Step 4: Apply the Nernst equation
The Nernst equation at room temperature (298 K) is given by:
E=E∘−0.0591nlog(products)(reactants)
For the anode reaction:
- n=2 (since 2 electrons are transferred)
- The concentration of H2 is 1 atm (standard condition).
The Nernst equation for the anode becomes:
Eanode=0−0.05912log(H+)21
Step 5: Substitute known values
Substituting the values we have:
0.151=−0.05912log(H+)2
This simplifies to:
0.151=−0.02955log(H+)2
Step 6: Solve for (H+)
Rearranging gives:
log(H+)2=−0.1510.02955
log(H+)2=−5.11
Taking the antilog:
(H+)2=10−5.11
(H+)=10−2.555
Step 7: Calculate pH
Since pH is defined as:
pH=−log(H+)
We find:
pH=−log(10−2.555)
pH≈2.555
Final Answer
The calculated pH value is approximately:
pH≈2.5
The cell is represented as:
Pt(H2)(1 atm)|H+(pH=?)|AgI(s),Ag
H2→2H++2e−
AgI+e−→Ag+I−
- The standard electrode potential for the cathode reaction (AgI + e^- → Ag + I^-) is given as:
E∘cathode=−0.151 V
E∘anode=0 V
The EMF of the cell is given as:
Ecell=Ecathode+Eanode
0=−0.151+Eanode
Thus, we can find Eanode:
Eanode=0.151 V
The Nernst equation at room temperature (298 K) is given by:
E=E∘−0.0591nlog(products)(reactants)
- n=2 (since 2 electrons are transferred)
- The concentration of H2 is 1 atm (standard condition).
Eanode=0−0.05912log(H+)21
Substituting the values we have:
0.151=−0.05912log(H+)2
0.151=−0.02955log(H+)2
Rearranging gives:
log(H+)2=−0.1510.02955
log(H+)2=−5.11
(H+)2=10−5.11
(H+)=10−2.555
Since pH is defined as:
pH=−log(H+)
We find:
pH=−log(10−2.555)
pH≈2.555
The calculated pH value is approximately:
pH≈2.5
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE-0235videos
ELECTROCHEMISTRY
- BOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE-0324videos
ELECTROCHEMISTRY
- BOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - INTEGER TYPE18videos
ELECTROCHEMISTRY
- BOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - ORGANIC CHEMISTRY472videos
CHEMISTRY AT A GLANCE
- BOOK - ALLENCHAPTER - HYDROCARBONEXERCISE - MCQ15videos
HYDROCARBON
Similar Questions
For the cell Pt(s),H2(1atm)∣∣H+(pH=2)∣∣∣∣H+(pH=3)∣∣H2(1atm),Pt
The cell reaction isView SolutionPt(H2)(1atm)∣H2O, electrode potential at 298K is
View SolutionAg++e−→Ag,E0=+0.8VandZn2++2e−→Zn,E0=−076V. Calculate the cell potential for the reaction, 2Ag+Zn2+→Zn+2Ag+
View SolutionPt∣∣∣(H2)1atm∣∣∣pH=2∣∣∣∣∣∣pH=3∣∣∣(H2)Pt1atm∣∣∣. The cell reaction for the given cell is:-
View SolutionThe cell Pt|H2(g)(1atm)|H+,pH=x∣∣∣ Normal calomal electrode has EMF of 0.64 volt at 25∘C. The standard reduction potential of normal calomal electrode is 0.28V. What is the pH of solution in anodic compartment. Take 2.303RTF=0.06 at 298K.
View SolutionThe pKsp of AgI is 16.07 if the E∘ value for Ag+/Ag is 0.7991V, find the E∘ for the half cell reaction AgI(s)+e−→Ag+I−
View SolutionThe emf of the cell, Pt|H2(1atm)|H+(0.1M,30mL)∣∣Ag+(0.8M)Ag is 0.9V. Calculate the emf when 40mL of 0.05MNaOH is added.
View SolutionThe oxidation potential of a hydrogen electrode at pH=10 and pH2=1atm is
View SolutionThe emf of the cell involving the following reaction, 2Ag++H2→2Ag+2H+ is 0.80 volt. The standard oxidation potential of silver electrode is:-
View SolutionFor the half cell,
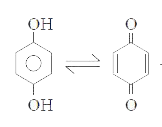
+2H+2e−.E0=
1.30 V. At pH=2, electrode potential of the given quinhydrone half cell is :View Solution

