Three identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
1.67×10−11(ˆi+ˆj)N
3.34×10−10(ˆi+ˆj)N
1.67×10−9(ˆi+ˆj)N
3.34×10−10(ˆi−ˆj)N
The correct Answer is:C
To solve the problem of finding the net gravitational force on the mass at the origin due to the other two masses, we can follow these steps:
Step 1: Identify the positions of the masses
- Mass 1 (m1 = 1 kg) is located at the origin (0, 0).
- Mass 2 (m2 = 1 kg) is located at (0, 0.2 m).
- Mass 3 (m3 = 1 kg) is located at (0.2 m, 0).
Step 2: Calculate the gravitational forces acting on the mass at the origin
The gravitational force between two point masses is given by the formula:
F=G⋅m1⋅m2r2
where:
- G is the gravitational constant ≈6.67×10−11N m2/kg2,
- m1 and m2 are the masses,
- r is the distance between the masses.
Step 3: Calculate the force due to mass 2
- The distance r12 between mass 1 and mass 2 is 0.2 m.
- Using the formula:
F12=G⋅m1⋅m2r212=6.67×10−11⋅1⋅1(0.2)2
F12=6.67×10−110.04=1.6675×10−9N
- This force acts downward (negative y-direction).
Step 4: Calculate the force due to mass 3
- The distance r13 between mass 1 and mass 3 is also 0.2 m.
- Using the formula:
F13=G⋅m1⋅m3r213=6.67×10−11⋅1⋅1(0.2)2
F13=6.67×10−110.04=1.6675×10−9N
- This force acts to the left (negative x-direction).
Step 5: Determine the net gravitational force
- The net gravitational force →Fnet on the mass at the origin is the vector sum of →F12 and →F13:
→Fnet=−F12^j−F13^i
→Fnet=−1.6675×10−9^j−1.6675×10−9^i
Step 6: Express the net force in component form
- The net force can be expressed as:
→Fnet=−1.6675×10−9^i−1.6675×10−9^j
Step 7: Final result
- The magnitude of the net gravitational force can be calculated as:
|→Fnet|=√(−1.6675×10−9)2+(−1.6675×10−9)2
|→Fnet|=√2⋅(1.6675×10−9)2=1.6675×10−9√2
- The final expression for the net gravitational force is:
→Fnet=−1.6675×10−9(^i+^j)
- Mass 1 (m1 = 1 kg) is located at the origin (0, 0).
- Mass 2 (m2 = 1 kg) is located at (0, 0.2 m).
- Mass 3 (m3 = 1 kg) is located at (0.2 m, 0).
The gravitational force between two point masses is given by the formula:
F=G⋅m1⋅m2r2
where:
- G is the gravitational constant ≈6.67×10−11N m2/kg2,
- m1 and m2 are the masses,
- r is the distance between the masses.
- The distance r12 between mass 1 and mass 2 is 0.2 m.
- Using the formula:
F12=G⋅m1⋅m2r212=6.67×10−11⋅1⋅1(0.2)2
F12=6.67×10−110.04=1.6675×10−9N
- This force acts downward (negative y-direction).
- The distance r13 between mass 1 and mass 3 is also 0.2 m.
- Using the formula:
F13=G⋅m1⋅m3r213=6.67×10−11⋅1⋅1(0.2)2
F13=6.67×10−110.04=1.6675×10−9N
- This force acts to the left (negative x-direction).
- The net gravitational force →Fnet on the mass at the origin is the vector sum of →F12 and →F13:
→Fnet=−F12^j−F13^i
→Fnet=−1.6675×10−9^j−1.6675×10−9^i
- The net force can be expressed as:
→Fnet=−1.6675×10−9^i−1.6675×10−9^j
- The magnitude of the net gravitational force can be calculated as:
|→Fnet|=√(−1.6675×10−9)2+(−1.6675×10−9)2
|→Fnet|=√2⋅(1.6675×10−9)2=1.6675×10−9√2
- The final expression for the net gravitational force is:
→Fnet=−1.6675×10−9(^i+^j)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 2 (Brain Teasers)27videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)20videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)46videos
KINEMATICS-2D
Similar Questions
A large number of identical point masses m are placed along x - axis ,at x = 0,1,2,4,……… The magnitude of gravitational force on mass at origin ( x =0) , will be
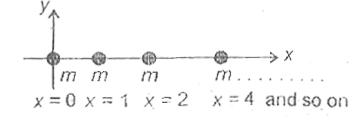 View Solution
View SolutionTwo bodies of masses 10 kg and 20 kg are located in x-y plane at (0, 1) and (1, 0). The position of their centre of mass is
View SolutionTwo bodies of masses 0.5 kg and 1 kg are lying in the X-Y plane at points (-1, 2) and (3, 4) respectively. Locate the centre of mass of the system.
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass isView SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree balls each of mass 0.5 kg are kept at the vertices of an isosceles right triangle with its hypotenuse of 2√2 m. What will be the net gravitational force on the ball kept at the vertex of right angle ?
View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionThe gravitational field in a region is given by →E=(5Nkg−1)→i+(12Nkg−1)→j.. a. find the magnitude of the gravitational force acting on a particle of mass 2 kg placed at the origin b. Find the potential at the points (12m,0) and (0,5m) if the potential at the origin is taken to be zero. c. Find the change in gravitational potential energy if a particle of mass 2 kg is taken from the origin to the point (12m,5m). d. Find the change in potential energy if the particle is taken from (12m,0) to (0,5m).
View SolutionTwo small particles P and Q each of mass m are fixed along x-axis at points (a,0) and (-a,0). A third particle R is kept at origin. Then
View SolutionThe gravitational force on a body of mass 1.5 kg situated at a point is 45 M . The gravitational field intensity at that point is .
View Solution

